How to calculate magnetic vector potential?

[tim9000]

Source WIki:
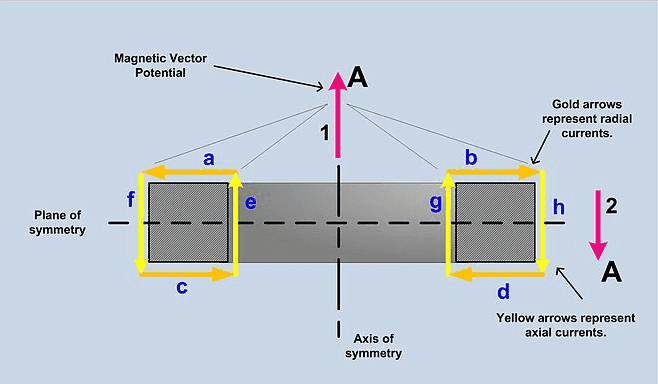
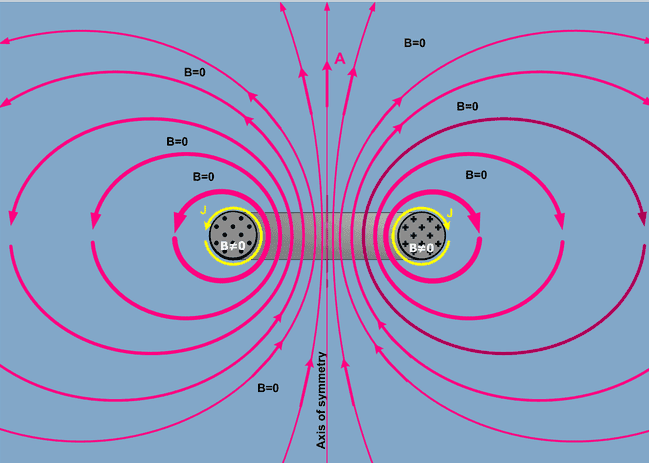
An axially symmetric toroidal inductor with no circumferential current totally confines the B field within the windings, the A field (magnetic vector potential) is not confined. Arrow #1 in the picture depicts the vector potential on the axis of symmetry. Radial current sections a and b are equal distances from the axis but pointed in opposite directions, so they will cancel. Likewise segments c and d cancel. In fact all the radial current segments cancel. The situation for axial currents is different. The axial current on the outside of the toroid is pointed down and the axial current on the inside of the toroid is pointed up. Each axial current segment on the outside of the toroid can be matched with an equal but oppositely directed segment on the inside of the toroid. The segments on the inside are closer than the segments on the outside to the axis, therefore there is a net upward component of the A field along the axis of symmetry.

The E and B fields can be computed from the A and

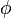(scalar electric potential) fields

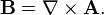[8] and :

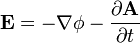[8] and so even if the region outside the windings is devoid of B field, it is filled with non-zero E field.
The quantity

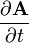is responsible for the desirable magnetic field coupling between primary and secondary while the quantity

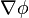is responsible for the undesirable electric field coupling between primary and secondary.What I'm wondering is how do you actually calculate 'A' the mag vector potential in the first place?

Thanks

 

[Baluncore]

Follow the links to; https://en.wikipedia.org/wiki/Magnetic_potential#Calculation_of_potentials_from_source_distributions

 

[tim9000]

Follow the links to; https://en.wikipedia.org/wiki/Magnetic_potential#Calculation_of_potentials_from_source_distributions

Thanks for the reply Baluncore, do you think you could help me put that equation in perspective. Say you're putting a current through the red wire of some number N turns below, you've got B inside the core, so A is up through the centre of the toroid which we say is the z-axis. You'd have a 'J' current (density?) circling like in the previous picture but as far as that equation is concerned, is that the current (density) flowing through the wire? (which we can measure with an ammeter and calculate the J from the diamter of the wire)
And how do or should I define r the position vector? Should the defined origin be along the z-axis and if so should z = 0 be in the middle of the toroid, so O(0,0,0)?

Any chance you should show me a dummy example of evaluating that expression for A? I'm having a bit of trouble understanding it. What does that d³ mean, is it a triple integral?
Thank you

 

[dlgoff]

... should I define r the position vector? ... What does that d³ mean, ...

Yes, r is the position vector from a current density volume element to a vector potential point of interest; d³r is the current density volume element. A is not just along the Z-axis.

image compliments of http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magvec.html

 

[tim9000]

Yes, r is the position vector from a current density volume element to a vector potential point of interest; d³r is the current density volume element. A is not just along the Z-axis.

image compliments of http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magvec.html

That is a helpful post, thanks. Glad to know I don't have to do a triple integral. Say I defined the point of origin halfway in the toroid on the centre axis as below (A is in the z direction):

So the 'current density volume element' in my case that's the (red) current carrying wire wraped around the toroid right? Not some currend flowing in the surface of the toroid? I''m still having trouble adapting my model to your equation because in mine the current is circeling the toroid vertically on the Z-Y plane and only makes one turn on the X-Y plane every 360^o and in practice I'd cancel that out with a retrun wire so I want to ignore that. In yours the current is circling on the X-Y plane.So J would be the current 'I' in the wire divided by the cross secional area of the wire?
If so what does this mean for dS and dl?
Thanks!

 

[dlgoff]

dS is the toroids cross-sectional area (see your first picture; the area contained in afce) and dl is the infinitesimal distance as you integrate around the toroid.

 

[tim9000]

dS is the toroids cross-sectional area (see your first picture; the area contained in afce) and dl is the infinitesimal distance as you integrate around the toroid.

Yeah but the difference is that toroid has the A vector tangential to the toroid and mine has the A vector pointing up inside the toroid and down outside. So it's kind of like the toroid in that picture on it's side rotated 360^o, for each turn of the wire around another toroid core. but in my case the wire is a rectangle not a toroid as in your picture. That's why I thought dS might have been the cross sectional area of the wire.

So what do I do for 'r' for some arbitary point on the z-axis? I assume r is all the same magnitude on everywhere on the z-axis? And does that mean in my case:
A = μ₀/4π * (j current density of wire) * (cross sectional area of toroid) * 2π*(mid toroid radius) / r
I was thinking I don't need to integrate around dl because it's a circle, hence the 2π*radius?

Should r be the same as the middle of the toroid radius? (in which case they'd cancel out) Or perhaps dl is 2h+2R in my diagram? (where R is the width of the toroid as in the diagram)
In which case it would be: A = μ₀/4π * (j current density of wire) * (cross sectional area of toroid) * (2h + 2R) / r

Remember about those gold arrows in the first picture that it says "The axial current on the outside of the toroid is pointed down and the axial current on the inside of the toroid is pointed up. Each axial current segment on the outside of the toroid can be matched with an equal but oppositely directed segment on the inside of the toroid. The segments on the inside are closer than the segments on the outside to the axis, therefore there is a net upward component of the A field along the axis of symmetry."

You can see why I'm still not sure what the equation will be. I guess its like the A I'm looking for is the sum of the A from your equation.
Thanks a lot

 

[dlgoff]

I think you are confusing the toroid with a current loop.

1) The magnetic field from current in a straight wire:

2) The magnetic field from current in a loop of wire:

3) The magnetic field from current in a coil of wire:

Now if a coil is around a toroid, as you have in your situation, there's a magnetic field of the toroid.

You should now spend some time on these links and try to understand how the magnetic vector potential is determined anywhere in space relative to your toroid.

Perhaps there are other members here that can explain this better than I.

Edit: I'm having trouble getting the images to show up but you can find them in the referenced links I gave from http://hyperphysics.phy-astr.gsu.edu/hbase/Indxback.html

 

[tim9000]

I think you are confusing the toroid with a current loop.
1) The magnetic field from current in a straight wire:

2) The magnetic field from current in a loop of wire:

3) The magnetic field from current in a coil of wire:

Now if a coil is around a toroid, as you have in your situation, there's a magnetic field of the toroid.

You should now spend some time on these links and try to understand how the magnetic vector potential is determined anywhere in space relative to your toroid.

Perhaps there are other members here that can explain this better than I.

Edit: I'm having trouble getting the images to show up but you can find them in the referenced links I gave from http://hyperphysics.phy-astr.gsu.edu/hbase/Indxback.html

Yeah I'm already familiar with those examples, the problem is that those pictures are different than the instance I'm analylising, I think you're confusing what the toroid is in each case, as I said: 'the difference is that your toroid is the current wire, and has the A vector tangential to the toroid. Whereas mine has the A vector pointing up inside the toroid (as my toroid is the magnetic core) and A goes down outside the toroid. So it's kind of like the toroid in your picture is on it's side rotated 360deg (for each turn of the wire around another toroid core).'
Thanks anyway

 

[jim hardy]

Vector Calculus was the course that showed me the limit of my abilities. It drove me to my knees, i passed only by memorizing techniques i didn't understand. So take following with a grain of salt.

This image from Baluncore's link

is followed by this text

the lines and contours of A relate to B like the lines and contours of B relate to j. Thus, a depiction of the A field around a loop of B flux (as would be produced in a toroidal inductor) is qualitatively the same as the B field around a loop of current.

It'd take me days to figure out that vector calculus.

I'd start with this observation:
Red circles, A, appear to represent the external magnetic field of a toroid, outside the spiral winding.
It of course is way smaller than the field inside the spiral winding, along its axis.
Let's just pick that purple one on right half.
Mr Gauss tells us that closed loop integral of h dot dl = current enclosed.
I can accept that because it's how a clamp-on ammeter works.
So if i walk that purple circle have i enclosed any current ?
Why yes, because the current in that winding has corkscrewed its way from in front of the paper to behind the paper.
Viewed from the top the current in the winding would corkscrew its way completely around the toroid, counterclockwise.
That amounts to one turn in the plane of the toroid.
And that's why toroids can have a small external field.
Some folks wind one turn around the toroid in the direction to cancel out that mmf from the corkscrew current's one turn in plane of core.

When the formula that i derive reflects that observation, i would have confidence i'd done it correctly .
But until then i'd know vector calculus was still mastering me , not the other way 'round.

Does that help any ?

Not some currend flowing in the surface of the toroid?

That corkscrew current indeed is equivalent to a current flowing around toroid's surface or maybe even at its centroid in cross section . I'll guess the math would say surface or centroid give same result. Biot-Savart ?

VC is my valley of death and i am sore afraid of it.

old jim

 

[tim9000]

Vector Calculus was the course that showed me the limit of my abilities. It drove me to my knees, i passed only by memorizing techniques i didn't understand.
Does that help any ?

Thanks Jim,
Yes, in that image you reference B is inside a core, so A is coming out like a corkscrew (right hand rule)
Did you see the image:

Just assuming that B is canceled externally, and is confined internally, the B in my example in my 2nd and 3rd posts is caused by a current in a wire wrapped around the toroid (the gold arrows) and the wiki article states about that above picture "Arrow #1 in the picture depicts the vector potential on the axis of symmetry. Radial current sections a and b are equal distances from the axis but pointed in opposite directions, so they will cancel. Likewise segments c and d cancel. In fact all the radial current segments cancel. The situation for axial currents is different. The axial current on the outside of the toroid is pointed down and the axial current on the inside of the toroid is pointed up. Each axial current segment on the outside of the toroid can be matched with an equal but oppositely directed segment on the inside of the toroid. The segments on the inside are closer than the segments on the outside to the axis, therefore there is a net upward component of the A field along the axis of symmetry."
So I don't know if full-on vector calculus to calculate A is necessary. (I'm interested in calculating A because I want to calculate the B field flowing inside the toroid from B = ∇xA)

dlgoff gave a nice formula for A in his first post which I think I can apply, but as in my 3rd post I'm just not sure how the variables interchange. Because the difference between the formula in his current loop and mine is that his toroid IS the current wire, and has the A vector of that is tangential to his toroid (the current path). Whereas my toroid is a magnetic core and has the A vector pointing up inside the toroid and A goes down outside the toroid (as the above wiki quote explains). So it's kind of like the toroid in his formula is on it's side rotated 360deg around my magnetic core (that is his toroid is each turn of the wire around another toroid core, the golden arrows making a rectangle in the aboe picture).

Does that clarify my point, or am I wrong about something?
Thanks again for the input!

 

[jim hardy]

Caution: this post was written under the mis-conception that A was some form of mmf , not "magnetic vector potential" which it turns out has quite a different meaning.
sorry about that, old jimMy bifurcated brain has two hangups that'll take me a few hours to resolve. I mention them so you'll understand my plight.

1. In top picture post 10 we have current density j, in bottom picture post 11 we have current i. There are more square inches on the outside of a toroid than on the inside, so if amps per square inch is same both inside and out then how do i square that with Kirchoff?
Chewing on that as we speak. Expect resolution when go out to work on my TV antenna for my alleged brain thinks best in background..

2. This picture dlgoff linked shows current flowing around the donut core in a circle, in one plane.
In fact a toroid has such a current because the winding progresses all the way around the core, just it's not a nice circular path but a spiral path that encircles the core. Imagine cutting the core and straightening it out - it's an electromagnet with winding along its whole length.

Now when i look at the picture you posted in 11, my alleged brain jumps to this thought experiment:
What if those two current loops afce and bhdg were not part of a spiral winding that circumnavigates the toroid , instead were single turns in the plane of the paper powered by individual batteries?
Now there'd be no current traversing the circumference of the toroid, only those two loops n the same plane.
So my closed loop integral(i assume that;s what the circle in middle of ∫ sign means) should traverse those current loops in plane of paper, not the loop made by toroid core which goes behind and in front of the paper.
So the problem has changed. In right hand equation above, our dL is now rotated 90 degrees from what it was. Moving A out of the plane of the paper, into the plane of the toroid.

When i first looked at this image i said "something doesn't seem right."

Here's what it is.
Apply right hand rule to ANY of those eight yellow arrow currents.
All eight of them create mmf in toroid that's ccw viewed from above.
I don't see a vertical mmf component along A from the vertical currents, because the current loops are in the same plane as A loops.

and everywhere i look i see mmf only normal to plane of loop where it passes through that plane

(Sorry, image should be flipped so current loop is in plane of paper)
and if this formula is any good
http://www.netdenizen.com/emagnettest/offaxis/equation2.offaxisloop.img.png

then there is no radial component in the plane of the loop because anywhere in the plane of the loop ϒ is zero.

http://www.netdenizen.com/emagnettest/offaxis/equation1.offaxisloop.img.png

http://www.netdenizen.com/emagnettest/offaxis/equation2.offaxisloop.img.png
B is the magnetic field, in teslas, at any point in space that isn't on the current loop. It is equal to the sum of two field components:

Bx the magnetic field component that is aligned with the coil axis and

Br the magnetic field component that is in a radial direction.

i is the current in the wire, in amperes.

a is the radius of the current loop.

x is the distance, on axis, from the center of the current loop to the field measurement point.

r is the radial distance from the axis of the current loop to the field measurement point.

http://www.netdenizen.com/emagnettest/offaxis/equation3.offaxisloop.img.png

http://www.netdenizen.com/emagnettest/offaxis/equation4.offaxisloop.img.png

http://www.netdenizen.com/emagnettest/offaxis/equation5.offaxisloop.img.png

K(k) is the complete elliptic integral function, of the first kind.

E(k) is the complete elliptic integral function, of the second kind.

Note that the argument to K and E is shown here as the modulus "k". Other valid arguments are the parameter "m" (where m = k2) and the modular angle "α" (where α = sin-1k). Substitute the argument that is appropriate for the mathematical tool you are using.

Bo is the magnetic field at the center of the coil (iμo/2a)

μo is the permeability constant (1.26x10-6 H/m or 4πx10-7).

As always, units of linear dimension (a) and magnetic field (B) are adjustable by using an appropriate value for the permeability constant.

I'm condemned to this meager sort of understanding.

If I'm wrong please point it out.

So all that having been said ,

i reject this sentence

The segments on the inside are closer than the segments on the outside to the axis, therefore there is a net upward component of the A field along the axis of symmetry.

as bilgewater.

stricken paragraph was based on misconception A is mmf. I don't know what is A or how it's calculated , i withdraw the assertion of "bilgewater" jh

The upward mmf field results from the one effective turn in plane of core carrying current around that loop , aforementioned "corkscrew current".
Extreme quality toroid transformers wrap a single turn circumferentially around the whole core in direction to cancel that corkscrew mmf.

make sense ?

old jim

 

[jim hardy]

Sorry for typos above.

Congratulations to you and dlgoff, between you i learned quite a bit.. my alleged brain is smoldering now.

nice job all.
see also this link for off axis field.
https://www.wakari.io/sharing/bundle/ericdennison/magnets/Off Axis Field of a Current Loop.ipynb

i shouldn't whine so about vector calculus for i have highest respect and admiration for those who are able, and i woudn't want anyone to think otherwise.. just please don't anybody think I'm a resource for it.

old jim

 

[jim hardy]

In this toroid current I enters at left wire and exits at right wire, having circumnavigated the core ounterclockwise , albeit like a corkscrew ,
So by right hand rule there's I X one turn of mmf pushing flux up out of the page,

image at http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/toroid.html
i shudder at the thought of writing the equation for that spiral path.

that can be corrected so there's no net z axis mmf

from http://physics.stackexchange.com/qu...ly-confined-within-the-core-of-a-toroid-but-n

One can think of a toroid as a solenoid that has been curved and joined so no poles are open. A toroid can have magnetic fields outside its geometrical boundary according to the way the currents are flowing, if there is a circumferential current that has not been neutralized. Once neutralized there is magnetic field only inside.( as described in the link given above). A neutralizing design is shown below.

in this toroid, current entering on red wire progresses around the core clockwise making I X one turn of mmf as before, but this time into the page. Notice that red wire turns white and goes back around the core counterclockwise, that I X one turn cancels red wire's mmf.

That's why i think the wiki statement in post 1 about mmf resulting from different radii for inside vs outside of turns is wrong.

my mistake, wiki was talking abut "A" not about mmf
MMF appears because the direction of current flow has a circumferential component.

 

[tim9000]

In this toroid current I enters at left wire and exits at right wire, having circumnavigated the core ounterclockwise , albeit like a corkscrew ,
Soby right hand rule there's I X one turn of mmf pushing flux up out of the page,

in this toroid, current entering on red wire progresses around the core clockwise making I X one turn of mmf as before, but this time into the page. Notice that red wire turns white and goes back around the core counterclockwise, that I X one turn cancels red wire's mmf.

http://physics.stackexchange.com/qu...ly-confined-within-the-core-of-a-toroid-but-n

That's why i think the wiki statement in post 1 about mmf resulting from different radii for inside vs outside of turns is wrong.

I need to read your Post #12 again, I only just then skimmed through it, but I must admit I did have my doubts about the wiki statement, but keep in mind B is the Curl of A, (B inside the core). So even though I doubt it, I am still struggling to accept that it's "Bildgewater" yet. Maybe on reflecting on what you said again it'll click with me. Are you saying that there is no A on the axis of symmetry?
Flipping this all on it's head, say instead of calculating B from A maybe you did A from B, (would) the only otherway you were calculating B inside the core would be:
B = (Number of turns * Current / Reluctance ) / cross sectoinal area of core
wouldn't it?

 

[jim hardy]

Are you saying that there is no A on the axis of symmetry?

1. What the heck is "A" ? Is it a mmf? If so, where are the amp-turns? They're in the circumferential component of current in the spiral winding.
In this picture

there is no mmf in direction of red arrow A because there's no circumferential component in either of those gold rectangles.

In this picture (which was your link not baluncore's like i thought)

B is equated to zero, so no flux means no net mmf... so what the heck is A ? Have i missed not only the boat but the whole pier ?

 

[jim hardy]

B inside the core would be:
B = (Number of turns * Current / Reluctance ) / cross sectoinal area of core

that looks right. B X area = Φ = mmf/ℝ

old jim

 

[tim9000]

1. What the heck is "A" ? Is it a mmf? If so, where are the amp-turns? They're in the circumferential component of current in the spiral winding.
In this picture

there is no mmf in direction of red arrow A because there's no circumferential component in either of those gold rectangles.

In this picture (which was your link not baluncore's like i thought)B is equated to zero, so no flux means no net mmf... so what the heck is A ? Have i missed not only the boat but the whole pier ?

Hee hee hee, I'm still only half way through re-reading your post #12.
But A is the (vector) magnetic potential, I think of it as like when you imagine the current is your right thumb and the curl of your fingers is the B field circling around it. Same thing with A as far as I know, imagine A is your thumb and B is your fingers, or vice versa, as far as I know A is often parallel to current or like the tangent of B. I've just been going from this really:
http://www.feynmanlectures.caltech.edu/II_15.html

 

[dlgoff]

so what the heck is A ?

It's the magnetic vector potential that tim9000 is pondering.

 

[jim hardy]

just glanced at your feynman lecture

Using the vector potential is often more difficult for simple problems for the following reason. Suppose we are interested only in the magnetic field B at one point, and that the problem has some nice symmetry—say we want the field at a point on the axis of a ring of current. Because of the symmetry, we can easily get B by doing the integral of Eq. (15.25). If, however, we were to find A first, we would have to compute B from derivatives of A, so we must know what A is at all points in the neighborhood of the point of interest. And most of these points are off the axis of symmetry, so the integral for A gets complicated. In the ring problem, for example, we would need to use elliptic integrals. In such problems, A is clearly not very useful. It is true that in many complex problems it is easier to work with A, but it would be hard to argue that this ease of technique would justify making you learn about one more vector field.

We have introduced A because it does have an important physical significance. Not only is it related to the energies of currents, as we saw in the last section, but it is also a “real” physical field in the sense that we described above. In classical mechanics it is clear that we can write the force on a particle as

F=q(E+v×B),(15.26)
so that, given the forces, everything about the motion is determined. In any region where B=0 even if A is not zero, such as outside a solenoid, there is no discernible effect of A. Therefore for a long time it was believed that A was not a “real” field. It turns out, however, that there are phenomena involving quantum mechanics which show that the field A is in fact a “real” field in the sense we have defined it. In the next section we will show you how that works.

Missed the pier ? Heck, I'm in the wrong harbor...

Seems to me A is one step removed from H. A surrounds mmf just as mmf surrounds current.

Part of becoming wise is learning what it is that i don't know.
I have to leave such math to the children of greater gods.

I'm sorry. Hope i didn't distract you from your studies.old jim

 

[tim9000]

just glanced at your feynman lecture
Missed the pier ? Heck, I'm in the wrong harbor...

Seems to me A is one step removed from H. A surrounds mmf just as mmf surrounds current.

Part of becoming wise is learning what it is that i don't know.
I have to leave such math to the children of greater gods.

I'm sorry. Hope i didn't distract you from your studies.

old jim

Hi Jim, no worries, your input is still helpful as it puts my own evaluation and comprehention into perspective.

 

[jim hardy]

i've edited post 12 and withdrawn the "bilgewater" assertion,

old jim < chagrin icon >