- #1
henry wang
- 30
- 0
How is pi/L part deduced in (n*pi*x)/L?
henry wang said: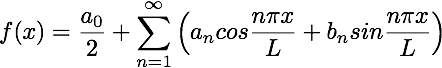
How is pi/L part deduced in (n*pi*x)/L?
The constant pi/L in Fourier series is a scaling factor that is used to normalize the trigonometric functions in the series. It is also known as the fundamental frequency or the Nyquist frequency.
The value of pi/L is determined by dividing the period of the function by 2pi. This results in a value of 1/L, which is then multiplied by pi to obtain the constant pi/L.
The constant pi/L is important in Fourier series because it allows for the accurate representation of a periodic function as a sum of sine and cosine functions. It also helps in determining the amplitudes and frequencies of these functions.
Yes, the value of pi/L can change in different Fourier series depending on the period of the function being analyzed. It is a constant that is specific to each function and is used to ensure that the series is correctly scaled.
The constant pi/L has no effect on the convergence of Fourier series. It is simply a scaling factor and does not alter the convergence properties of the series. The convergence of Fourier series depends on the smoothness and continuity of the function being analyzed.