- #1
pepediaz
- 51
- 6
- Homework Statement
- Not homework exactly :-[
- Relevant Equations
- H = T + U (I posted an attempt to the solution below)
Let a mass m charged with q, attached to a spring with constant factor k = mω ^2 in an electric field E(t) = E0(t/τ) x since t=0.
(Equilibrium position is x0 and the deformation obeys ξ = x - x0)
What would the hamiltonian and motion equations be in t ≥ 0, in terms of m and ω?? Despise magnetic field.
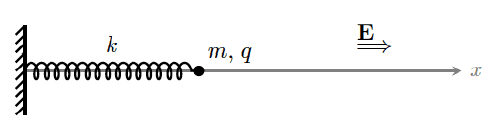
(Equilibrium position is x0 and the deformation obeys ξ = x - x0)
What would the hamiltonian and motion equations be in t ≥ 0, in terms of m and ω?? Despise magnetic field.
Last edited: