- #1
Adwit
- 15
- 2
- TL;DR Summary
- This problem is from the book "The Geometry Of Special Relativity" written by Tevian Dray. How is the distance function formula come from? Does it have any proof?
Can anyone derive the distance formula of a hyperbola for me, please? I have not found the derivation on the internet. I can't get any clue from the picture of hyperbola.
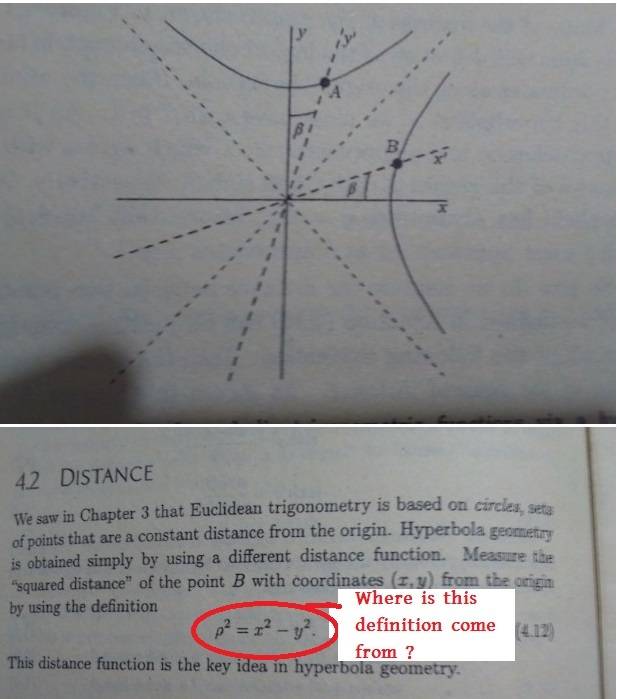
Last edited:

