Homology of Connected Sum of Two Projective Planes, P^2 # P^2

[Math Amateur]

I am reading James Munkres' book, Elements of Algebraic Topology.

Theorem 6.5 on page 39 concerns the homology groups of the connected sum of two projected planes.

Munkres demonstrates the following:

[itex] H_1 ( P^2 \# P^2 ) \simeq \mathbb{Z} \oplus \mathbb{Z} / 2 [/itex] ... ... ... (1)

and

[itex] H_2 ( P^2 \# P^2 ) = 0 [/itex] ... ... ... (2)

I would appreciate some help in understanding how Munkres establishes [itex] H_2 ( P^2 \# P^2 ) = 0 [/itex]. He does this moderately early in the proof after setting up the definitions and notation.

The Theorem and the early part of the proof up to the statement that "it is clear that [itex] H_2 ( P^2 \# P^2 ) = 0 [/itex]" is as follows:

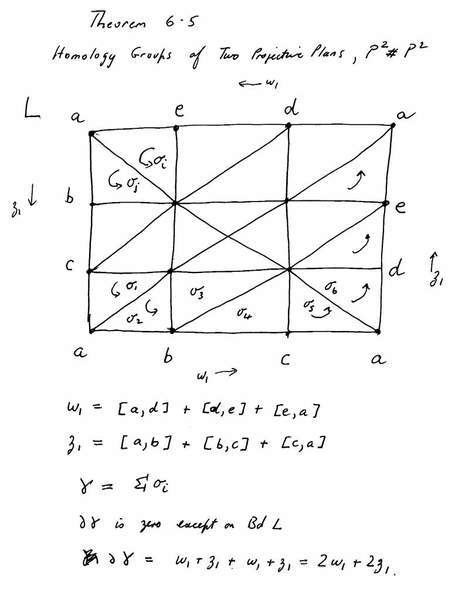
I have labelled L in a manner that I think is appropriate as follows:

Early in the proof (see above) Munkres refers to conditions 1 and 2. These conditions are as follows:

As I mentioned above, Munkres states, early in the proof, that

"It is clear that [itex] H_2 ( P^2 \# P^2 ) = 0 [/itex]"

BUT ... this is anything but clear to me ...

Can anyone explain why this 'clearly' follows:

Would appreciate some help.

Peter

 

[WWGD]

Sorry, I cannot read your post because it does not fit my screen, but there is a standard result that the top homology over a coefficient ring is 0 iff the space is not orientable, and the homology equals the coefficient ring the space is orientable. The homology of the connected sum is, I think the direct sum of the homology of the spaces, because you can glue your spaces so that the essential curves of each space stay within that space.

 

[Math Amateur]

Thanks for the help ... will work on what you have said ...

Pity you cannot read the post ... not sure what I can do to improve readability ...

There is a version of my post on Math Help Boards, Topology and Advanced Geometry forum ...

Math Help Boards is here ...

http://mathhelpboards.com/

and the forum concerned is here

http://mathhelpboards.com/topology-advanced-geometry-13/

Any help you (or anyone) can provide regarding Munkres' logic in the above post in achieving the conclusion [itex] H_2 (P^2 \# P^2 ) = 0 [/itex] would be very much appreciated.

Thanks again for the help

Peter

 

[WWGD]

O.K, I will look into the board.Sorry, I don't have Munkres ( nor his book :) ) available. I am at home; I will check my school's library.

Just curious: are you considering the algebraic method, or a purely topological one? From the algebra perspective, it comes down to finding the quotient:

## H_n:=Ker (d_n ) / I am (d_{n+1}) ##

i.e., n-cycles mod (n+1)-boundaries. I hope I am not telling you something you already know; maybe understanding this perspective will be helpful to you; sorry if it is not, or if you already know this. The general idea here is to
have the algebraic aspect reflect/reveal/ be-parallel-to the geometry of the space. Informally, a cycle c(geometrically) bounds in the space X if, removing the cycle disconnects the space; this is modeled algebraically by the machinery of cycles and boundaries. One of the connected components A,B left when the space is disconnected by removing c , i.e., X-c= A\/B is the subspace being bounded by c . Maybe the Jordan curve theorem is in play in here. You see, e.g., a cycle , i.e., a s.c.c ( simple-closed curve) going around T^2 , i.e., a parallel, does not bound any subspace of the torus; try removing it (if you cannot see it, do it physically) and notice that removing it will not disconnect the torus. But notice that, e.g., for the 2-sphere , if you remove any s.c.c, you will disconnect the space.

If you feel stuck with Munkres' approach, why not try, if you have it available, John Hocking's "Topology" , or some other text?

 

[Math Amateur]

Thanks WWGD ... appreciate the help ...

You write:

"O.K, I will look into the board.Sorry, I don't have Munkres ( nor his book :) ) available. I am at home; I will check my school's library."

Thanks!

You also write:

"Just curious: are you considering the algebraic method, or a purely topological one? From the algebra perspective, it comes down to finding the quotient:"

If you read Chapter 1 of Munkres, Elements of Algebraic Topology you will find his approach in Theorems 6.1 to 6.5 is largely topological and geometric.

Just now reflecting on the rest of your post ... and re-reading Munkres ...

Any further insights you get on Theorem 6.5 would be really welcome!

BTW, I do have the book Topology by Hocking and Young - will have a closer look at its treatment of simplicial homology. At first glance, Munkres looks easier to follow - but maybe I am fooing myself!

Thanks again,

Peter