First order approx. for a curve

[DaveC426913]

TL;DR Summary

Is there a simple function that would produce a curve in this family?

Helping someone with some fictional physics.

He's looking for a function that will produce a curve similar to this (poor geometry is my doing, assume smooth curvature):

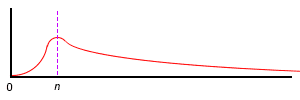
Starts at 0,0.
Maximum at n.
Reaches zero at infinity.
The cusp is not sharp, it's a curve (which, I think suggests at least two variables?).

Presumably, the curve is symmetrical about n logarithmically, but not a given.

 

[andrewkirk]

The lognormal pdf curve matches the four criteria listed, as do a number of other right-skewed, long-tailed probability distributions (could try pareto, weibull).

It has two parameters ##\mu,\sigma## that can be adjusted to modify the shape.

To make the maximum (mode of the distribution) happen at ##x=n## we set a constraint:

$$n=\mu-\sigma^2$$

 

[DaveC426913]

The lognormal pdf curve matches the four criteria listed, as do a number of other right-skewed, long-tailed probability distributions (could try pareto, weibull).

It has two parameters that can be adjusted to modify the shape.

Heh. I literally just stumbled upon this before tabbing back here.

 

[mfb]

##x^n e^{-cx}##
It starts at 0,0, it has a maximum at x=n/c, it goes to zero for x to infinity.

If the logarithmic property is required, ##e^{-\log(x/n)^2}## will do the job (it's just a normal distribution adjusted using log(x)), but it's a bit more complicated.

 

[DaveC426913]

##x^n e^{-cx}##
It starts at 0,0, it has a maximum at x=n/c, it goes to zero for x to infinity.

If the logarithmic property is required, ##e^{-\log(x/n)^2}## will do the job (it's just a normal distribution adjusted using log(x)), but it's a bit more complicated.

Thanks. What is c?

Also,where can I plug this into see it?

 

[FactChecker]

Thanks. What is c?

You should start with the fact that you want the peak to be at n. THIS IS NOT NECESSARILY THE n IN NBF'S POST. Using ##y= x^m e^{-cx}##, the peak is at ##m/c=n## (your ##n##). So you have a new function, ##y= x^{nc} e^{-cx}## with only the parameter, ##c##.

Also,where can I plug this into see it?

I like the free download of GeoGebra. It is easy to type in an equation and get a plot. In this case, you would want to first set up a parameter, c, and set the integer, n, to a value. Then define the function ##y= x^{nc} e^{-cx}##.
Here is an example.

 

[mfb]

Thanks. What is c?

An adjustable parameter. The ratio n/c is the position of the peak.

Example plots, both with their peak at x=1. I multiplied the second example by 3 for better comparison.

 

[FactChecker]

Here is a GeoGebra example of the lognormal method. Suppose you want the maximum value to be at n=2. That is the ##mean## of the lognormal distribution. So ##mean=2##. The lognormal has two parameters: ##NormMean## and ##NormVariance##. You can set the ##NormVariance \gt 0## parameter as you wish. The smaller you make it, the higher the maximum at n=2. The value of ##NormMean## is calculated as ##NormMean = ln(mode)+NormVariance^2##. With these parameters set, the lognormal PDF is determined. Here is the GeoGebra example.

 

[FactChecker]

To make the maximum (mode of the distribution) happen at ##x=n## we set a constraint:

$$n=\mu-\sigma^2$$

I think that should be ##n=e^{\mu-\sigma^2}##

 

[DaveC426913]

Thanks all.

 

[Svein]

What you have drawn looks like a Poisson distribution to me ...

 

[DaveC426913]

What you have drawn looks like a Poisson distribution to me ...

No.

This, sir, is a Poisson Distribution:

*_{for clarity that's a moustache, beret and ascot on a cod.}