- #1
Scholar1
- 39
- 0
Member warned about posting without the template
I have posted my attempt and the problem above. Please help!
Thanks in advance!
It's hard to mark up an image.Scholar1 said: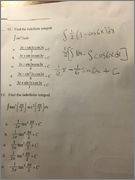
I have posted my attempt and the problem above. Please help!
Thanks in advance!
Yesss...multiplication distributes over addition and subtraction.Scholar1 said:So if I put - (1/12) in front of the sin6x it would be correct?
An indefinite integral is a mathematical concept used in calculus to find the most general antiderivative of a function. It is represented by the symbol ∫ f(x) dx, where f(x) is the function being integrated and dx represents the variable of integration. The result of an indefinite integral is a family of functions, rather than a single value.
To solve an indefinite integral problem, you need to use the rules of integration to find the antiderivative of the given function. These rules include the power rule, product rule, quotient rule, and chain rule. Once you have found the antiderivative, you can check your answer by taking the derivative of the result to see if it matches the original function.
The main difference between an indefinite integral and a definite integral is that a definite integral has specific limits of integration, while an indefinite integral does not. A definite integral also gives a numerical value as the result, while an indefinite integral gives a family of functions as the result.
Indefinite integrals have many real-world applications, including calculating the total distance traveled by an object given its velocity function, finding the total cost of a variable rate of production, and determining the amount of radioactive material remaining after a certain amount of time.
Yes, technology can be used to solve indefinite integral problems. Many graphing calculators and computer software programs have built-in integration functions that can quickly and accurately solve indefinite integrals. However, it is important to understand the concepts and rules of integration in order to use technology effectively and verify results.