- #1
cavalieregi
- 41
- 0
Hi I have the function
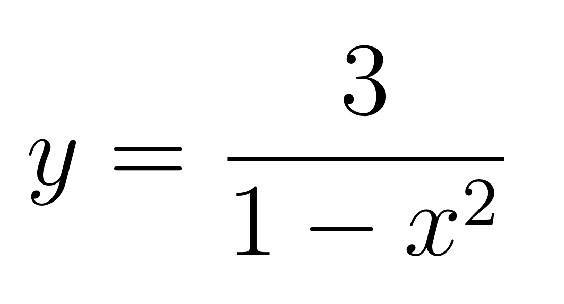
I have worked out the domain as not equal to 1 using the fact the denominator can't equal 0. Now I am stuck finding the range. How would I find it without graphing. The answer is y<0 , y=>3.
I have worked out the domain as not equal to 1 using the fact the denominator can't equal 0. Now I am stuck finding the range. How would I find it without graphing. The answer is y<0 , y=>3.