- #1
xio
- 11
- 0
[EDIT]: Correct answer for this problem is 1/2, not 4 as I thought before; that means the result for the explicit representation was correct. Still I don't understand how to treat the case with the parametric representation.
Greetings,
I need to evaluate $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS,$$ where ##S## is the plane surface whose boundary is the triangle with vertices at ##(1,0,0),(0,1,0),(0,0,1)## , ##\mathbf{F}(x,y,z)=(x,y,z)## , ##\mathbf{n}## is the unit normal to ##S## .
There are two representations for the surface:
and the general formula for this type of problems is $$\iint_{\mathbf{r}(T)}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}\mathbf{F}[\mathbf{r}(u,v)]\cdot\mathbf{n}\,\left\Vert \frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right\Vert \, du\, dv ,$$ but since $$\mathbf{n}=\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}/\left\Vert \frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right\Vert ,$$ it simplifies to $$\iint_{T}\mathbf{F}[\mathbf{r}(u,v)]\cdot\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\, du\, dv . $$
Parametric representation:
Given ##\mathbf{r}(u,v)=(u+v,u-v,1-2u) ##, we find $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}(u+v,u-v,1-2u)\cdot(-2,-2,-2)\, du\, dv=-2\iint_{T}\, du\, dv. $$ The problem now is that I simply cannot figure out the region of integration ##T## : ##0\leq1-2u\leq1## suggests that ##u\in[0,0.5]## ; taking this into account and the fact that ##0\leq u+v\leq1## , ##v\in[0,0.5]## . But now the two conditions imply that ##-0.5\leq u-v\leq0.5## , while it should be ##0\leq u-v\leq1## .
Explicit representation:
My best guess for the explicit representation of the surface is ##z=-x-y+1## (I omit its derivation here for brevity).
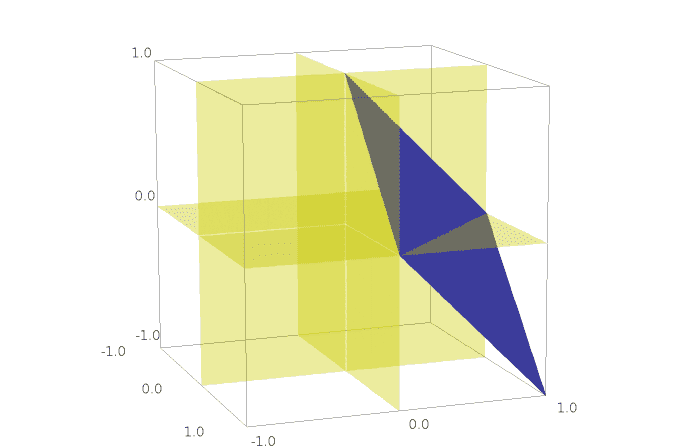
Hence $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}(x,y,-x-y+1)\cdot(1,1,1)\, dx\, dy=\iint_{T}\, dx\, dy .$$ Again I have troublems finding the region of integration. If it is the triangle on the ##z=0## plane, then ##x\in[0,1],y=1-x## and we have $$\iint_{T}\, dx\, dy=\int_{0}^{1}\left[\int_{0}^{1-x}dy\right]dx=1/2 ,$$ but the correct answer is “4” (I know it in advance).
Greetings,
I need to evaluate $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS,$$ where ##S## is the plane surface whose boundary is the triangle with vertices at ##(1,0,0),(0,1,0),(0,0,1)## , ##\mathbf{F}(x,y,z)=(x,y,z)## , ##\mathbf{n}## is the unit normal to ##S## .
There are two representations for the surface:
- parametric ##\mathbf{r}(u,v)=(u+v,u-v,1-2u) ##
- explicit ##z=f(x,y) ##
and the general formula for this type of problems is $$\iint_{\mathbf{r}(T)}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}\mathbf{F}[\mathbf{r}(u,v)]\cdot\mathbf{n}\,\left\Vert \frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right\Vert \, du\, dv ,$$ but since $$\mathbf{n}=\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}/\left\Vert \frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right\Vert ,$$ it simplifies to $$\iint_{T}\mathbf{F}[\mathbf{r}(u,v)]\cdot\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\, du\, dv . $$
Parametric representation:
Given ##\mathbf{r}(u,v)=(u+v,u-v,1-2u) ##, we find $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}(u+v,u-v,1-2u)\cdot(-2,-2,-2)\, du\, dv=-2\iint_{T}\, du\, dv. $$ The problem now is that I simply cannot figure out the region of integration ##T## : ##0\leq1-2u\leq1## suggests that ##u\in[0,0.5]## ; taking this into account and the fact that ##0\leq u+v\leq1## , ##v\in[0,0.5]## . But now the two conditions imply that ##-0.5\leq u-v\leq0.5## , while it should be ##0\leq u-v\leq1## .
Explicit representation:
My best guess for the explicit representation of the surface is ##z=-x-y+1## (I omit its derivation here for brevity).
Hence $$\iint_{S}\mathbf{F}\cdot\mathbf{n}\, dS=\iint_{T}(x,y,-x-y+1)\cdot(1,1,1)\, dx\, dy=\iint_{T}\, dx\, dy .$$ Again I have troublems finding the region of integration. If it is the triangle on the ##z=0## plane, then ##x\in[0,1],y=1-x## and we have $$\iint_{T}\, dx\, dy=\int_{0}^{1}\left[\int_{0}^{1-x}dy\right]dx=1/2 ,$$ but the correct answer is “4” (I know it in advance).
Last edited: