- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
I want to find the solution of the following initial value problem:
$$u_{tt}(x, t)-u_{xt}(x, t)=f(x, t), x \in \mathbb{R}, t>0 \\ u(x, 0)=0, x \in \mathbb{R} \\ u_t(x, 0)=0, x \in \mathbb{R}$$
using Green's theorem but I got stuck... I found the following example in my notes:
$$u_{tt}-c^2u_{xx}=f(x, t), x \in \mathbb{R}, t>0 \\ u(x, 0)=0, x \in \mathbb{R} \\ u_t(x, 0)=0, x \in \mathbb{R}$$
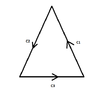
View attachment 4134
$$\iint_{\Omega}[u_{tt}(x, t)-c^2u_{xx}(x, t)]dxdt=\iint_{\Omega}f(x, t)dxdt=\int_0^{t_0} \left (\int_{x_0-ct_0+ct}^{x_0+ct_0-ct}f(x, t)dx\right )dt \tag 1$$
$$\iint_{\Omega}\left [\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{t}}\right ]dxdt=\int_{\partial{\Omega}}Pdx+Qdt$$
$$Q(x, t)=-c^2u_x \\ P(x, t)=-u_t$$
$$\iint_{\Omega}\left [u_{tt}(x, t)-c^2u_{xx}(x, t)\right ]dxdt=\int_{\partial{\Omega}}\left [-u_t(x, t)dx-c^2u_x(x, t)dt\right ]=\int_{C_1} [ \ \ ]+\int_{C_2} [ \ \ ]+\int_{C_3} [ \ \ ]$$
$(\int_{C_1} [ \ \ ]=cu(x_0, t_0), \int_{C_2} [ \ \ ]=cu(x_0, t_0), \int_{C_3} [ \ \ ]=0)$
View attachment 4135
$$\int_{C_3}[-u_t(x, 0)dx-c^2u_x(x, 0)dt], \text{ where } u_t(x, 0)=0, u_x(x, 0)=0$$ $$C_1: x+ct=x_0+ct_0 \Rightarrow dx+cdt=0$$
$$\int_{C_1}(-u_tdx-c^2u_xdt=\int_{C_1}-u_t(-cdt)-c^2u_x\left (-\frac{dx}{c}\right )=\int_{C_1}cu_tdt+cu_xdx=c \int_{C_1}u_tdt+u_xdx=c\int_{C_1}du=c(u(x_0, t_0)-u(x_0+ct_0, 0))\overset{ u(x_0+ct_0, 0)=0 }{ = }cu(x_0, t_0) \tag 2$$ $$2cu(x_0, t_0)=\int_0^{t_0}\int_{x_0-ct_0+ct}^{x_0+ct_0-ct}f(x, t)dx$$
$$u(x_0, t_0)=\frac{1}{2c}\iint_{c(x_0, t_0)}f(x, t)dxdt$$
I got stuck at the following:
Could you explain to me the first graph?? (Wondering)
Why are the limits of the integral at the relation $(1)$ the following: $x_0-ct_0+ct$ and $x_0+ct_0-ct$ ?? (Wondering)
Why does it stand at the relation $(2)$ that $u(x_0+ct_0, 0)=0$ ?? (Wondering)
I want to find the solution of the following initial value problem:
$$u_{tt}(x, t)-u_{xt}(x, t)=f(x, t), x \in \mathbb{R}, t>0 \\ u(x, 0)=0, x \in \mathbb{R} \\ u_t(x, 0)=0, x \in \mathbb{R}$$
using Green's theorem but I got stuck... I found the following example in my notes:
$$u_{tt}-c^2u_{xx}=f(x, t), x \in \mathbb{R}, t>0 \\ u(x, 0)=0, x \in \mathbb{R} \\ u_t(x, 0)=0, x \in \mathbb{R}$$
View attachment 4134
$$\iint_{\Omega}[u_{tt}(x, t)-c^2u_{xx}(x, t)]dxdt=\iint_{\Omega}f(x, t)dxdt=\int_0^{t_0} \left (\int_{x_0-ct_0+ct}^{x_0+ct_0-ct}f(x, t)dx\right )dt \tag 1$$
$$\iint_{\Omega}\left [\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{t}}\right ]dxdt=\int_{\partial{\Omega}}Pdx+Qdt$$
$$Q(x, t)=-c^2u_x \\ P(x, t)=-u_t$$
$$\iint_{\Omega}\left [u_{tt}(x, t)-c^2u_{xx}(x, t)\right ]dxdt=\int_{\partial{\Omega}}\left [-u_t(x, t)dx-c^2u_x(x, t)dt\right ]=\int_{C_1} [ \ \ ]+\int_{C_2} [ \ \ ]+\int_{C_3} [ \ \ ]$$
$(\int_{C_1} [ \ \ ]=cu(x_0, t_0), \int_{C_2} [ \ \ ]=cu(x_0, t_0), \int_{C_3} [ \ \ ]=0)$
View attachment 4135
$$\int_{C_3}[-u_t(x, 0)dx-c^2u_x(x, 0)dt], \text{ where } u_t(x, 0)=0, u_x(x, 0)=0$$ $$C_1: x+ct=x_0+ct_0 \Rightarrow dx+cdt=0$$
$$\int_{C_1}(-u_tdx-c^2u_xdt=\int_{C_1}-u_t(-cdt)-c^2u_x\left (-\frac{dx}{c}\right )=\int_{C_1}cu_tdt+cu_xdx=c \int_{C_1}u_tdt+u_xdx=c\int_{C_1}du=c(u(x_0, t_0)-u(x_0+ct_0, 0))\overset{ u(x_0+ct_0, 0)=0 }{ = }cu(x_0, t_0) \tag 2$$ $$2cu(x_0, t_0)=\int_0^{t_0}\int_{x_0-ct_0+ct}^{x_0+ct_0-ct}f(x, t)dx$$
$$u(x_0, t_0)=\frac{1}{2c}\iint_{c(x_0, t_0)}f(x, t)dxdt$$
I got stuck at the following:
Could you explain to me the first graph?? (Wondering)
Why are the limits of the integral at the relation $(1)$ the following: $x_0-ct_0+ct$ and $x_0+ct_0-ct$ ?? (Wondering)
Why does it stand at the relation $(2)$ that $u(x_0+ct_0, 0)=0$ ?? (Wondering)