Determining the direction of friction force on rolling

[Zalajbeg]

Hello everyone,

I cannot understand the logic behind determining the directions in the rolling problems. In all examples I have seen has a logic. Let us assume a rolling cylinder is moving to right as accelerating. If the cause of the acceleration is a torque the direction of the friction force is right. I can understand it as it is the only force exist and it has to be in the same direction as the acceleration.

In the examples I have seen another assumptation is that if the acceleration is because of a force (e.g. gravitational force on a inclined plane.) the friction force is in the opposite direction of this force. I don't understand why.

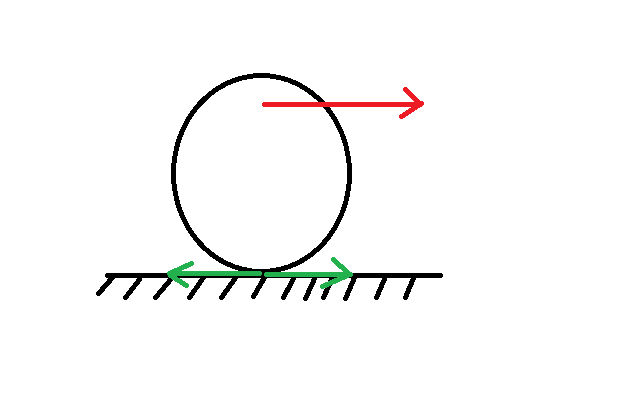
1) Let us assume I exert a force shown as the red. How can we know which one of the yellow ones will be the frictional force. Is there a mathematical way to prove this? (Maybe something about non-sliding condition but I want to see it mathematically)

2) Also I wonder how would I determine the direction if both a force and a torque existed.

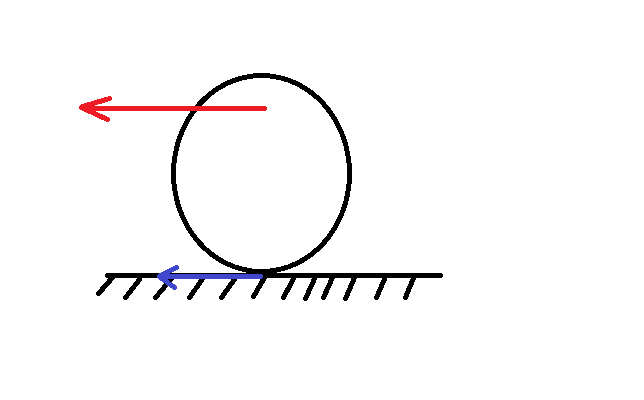
3) Let us say this time the rolling ressistance is not neglected and I am not trying to accelerate but deccelarate. (In the below image the red arrow shows the force I exert and the blue one shows the rolling deformation.) How can I determine the direction of the frictional force?

4) The last question is about the non-sliping condition. If I know the ressistance and friction forces and the coefficient of friction between the surface and the cylinder, how can I determine the maximum force I can exert without causing it to slip?

Thanks in advance!

 

[A.T.]

You already have a thread about this, why start a new one? Last time you seemed to get it:
https://www.physicsforums.com/threads/investigation-of-a-rotating-cylinder.770027/#post-4847396

 

[Zalajbeg]

Last time I just understood that the direction can vary for the different cases. However I noticed that I hadn't understood how to determine the direction.

By the way I have done some calculations. If I am not wrong the direction can be determined by the two equations:

[itex]F=m.a[/itex] and [itex]\tau =I\alpha [/itex]

Let me propose my findings on my first question. I assume the friction is in the same direction with the red one.

[itex]F-F_s=m.a[/itex]

[itex]Fr_o-F_sr=\frac {1}{2}m.r.a[/itex]

If I replace "m.a" in the second equation:

[itex]Fr_o-F_sr=\frac {1}{2}Fr-\frac {1}{2}F_sr[/itex]

[itex]F_s=\frac {F}{2} \frac {r_0-\frac {r}{2}}{r}[/itex]

Then I can conclude that if the right side is positive the direction is the same with the red force, otherwise the direction is opposite. I think I can find the answers of question 2 and 3 with the same approach.

For the force limit, I think the maximum static friction mustn't be exceed, otherwise it will slide

 

[A.T.]

If I am not wrong the direction can be determined by the two equations:

[itex]F=m.a[/itex] and [itex]\tau =I\alpha [/itex]

You also have to relate [itex]a[/itex] and [itex]\alpha [/itex], via the radius. That is the no silip boundary condition.

[itex]F - F_s = m.a[/itex]

I would recommend using vectors with the same sign convention, so it's:

[itex]F + F_s = m.a[/itex]

 

[Zalajbeg]

Thank you very much!

I have got one more question. As it is relevant to the topic it is better to ask it here instead of a new topic.

Let us assume, a vehicle is deccelerated by braking from the front wheels (the rear wheels are free). The vehicle deccelerates with an acceleration of "a". The rolling ressistance is neglected.

Then I wonder how the rear wheels can deccelerate. The only force I can see is the friction force. If it was the only force acting the linear acceleration would decrease but the angular acceleration would increase. Then it is certain that there is at least one more force. What is it? The inertial force of the vehicle (conducted via the axles)?

 

[A.T.]

Then I wonder how the rear wheels can deccelerate. The only force I can see is the friction force.

The axle exerts a backwards force on the wheels to brake them.

 

[Zalajbeg]

The axle exerts a backwards force on the wheels to brake them.

Is it only a force or will it be a force and a torque?

It seems the front axles exerts a force to the front wheels too. (This time it is forward) Will it be only a force or a force and a torque?

 

[A.T.]

Is it only a force or will it be a force and a torque?

If freewheeling on ideal bearings, there is no torque from it.

It seems the front axles exerts a force to the front wheels too. (This time it is forward) Will it be only a force or a force and a torque?

Depends how the braking of the front wheels is realized.

 

[Zalajbeg]

Thanks for your explanation. I wanted to do some calculations based on the knowledge I gained. It is about a vehicle braking. However I have a mistake somewhere and I cannot fnd it. Could you please check my steps?

My assumptations:

- The braking is done on a point over the wheel surface. The distance between the application point of the force F is r_f
- The problem is 2D. Therefore the calculations can be done with two wheels.
- There is no slip
- The mass of the vehicle is M and the mass of every wheel is m.
- The radius of the wheels are r.
- The bearings are not ideal, therefore there are both forces and torques from the axles to the wheels.

The below pictures are four free body diagrams, respectively the vehicle, the vehicle without weels, rear wheel and front wheel. They also show the equations associated with them. The directions of the forces and torques are arbitrary, the exact directions will be determined by the signs. Also I used the scalar forms.

F_s is the friction force, F_a and τ_a are the force and torque from the axle respectively.

Firstly it can be seen that the left sides of the equation 4 and the equation 6 is equal:

[itex]F_{s,2}+F_{a,2}=F_{s,1}+F-F_{a,1}[/itex]
[itex]F_{s,2}=F_{s,1}+F-F_{a,1}-F_{a,2}[/itex](***)

After that I am opening the equation 2:

[itex]F_{a,1}-F_{a,2}=Ma-2ma[/itex]

Then I am replacing "Ma" with the left side of the equation 1 and "ma" with the left side of the equation 4:

[itex]F_{a,1}-F_{a,2}=F_{s,1}+F_{s,2}-2F_{s,2}-2F_{a,2}[/itex]
[itex]F_{a,1}=F_{s,1}-F_{s,2}-F_{a,2}[/itex]

Finally, I replace F_s,2 with the right side of the equation (***).

[itex]F_{a,1}=F_{s,1}-F_{s,1}-F+F_{a,1}+F_{a,2}-F_{a,2}[/itex]
[itex]F=0[/itex]

However it is not the case, F is a force determined by me, it doesn't have to be zero. Could you please explain me in what step I am doing wrong?

 

[A.T.]

The braking is done on a point over the wheel surface. The distance between the application point of the force F is r_f

Who is applying F to the wheel? If the car, then (2) is wrong. If something external to the car, then (1) is wrong.

 

[Zalajbeg]

Who is applying F to the wheel? If the car, then (2) is wrong. If something external to the car, then (1) is wrong.

To you tell the truth, I didn't expect to get a clear answer only in one, short sentence. As it is the brake, the vehicle is applying it and the equation 2 is wrong. Thank you so much for finding it.

 

[Zalajbeg]

Who is applying F to the wheel? If the car, then (2) is wrong. If something external to the car, then (1) is wrong.

Hello again,

It seems I have one more problem. I don't know why but I always thought the seven equations above are independent but they are not. I have 7 unknowns and 6 independent equations. I need to reduce my unknowns by one. What can I do here?

You said there is no torque if the wheeling is free on the ideal bearings. Therefore I want to neglect this unknown. However this time it makes me think about this: If I ignore the torque in the rear wheels do I have to ignore it also on the front wheel? In a front wheel drive vehicle I am sure torque is transferred to the front wheels therefore it makes me think that there must be a torque also during the braking.

P.S: Actually I study on a thesis about calculating the temperature distribution on a brake disc. The calculations above are part of this work, I need to relate the pressure on the disc with acceleration. Therefore your help is very appreciated.

 

[A.T.]

In a front wheel drive vehicle I am sure torque is transferred to the front wheels therefore it makes me think that there must be a torque also during the braking.

Depends on how you brake (clutch state) and how accurately you want to model it.

 

[Zalajbeg]

Let us say I will not take the torque in the consideration, then I will have 6 equations and 5 unknowns will not it be a problem?

And can I say if the clutch is not pressed there is a torque, if not there is not?

 

[A.T.]

Let us say I will not take the torque in the consideration, then I will have 6 equations and 5 unknowns will not it be a problem?

If the equations are independent, then this indicates a problem in your assumptions, about which values can be freely chosen.

And can I say if the clutch is not pressed there is a torque, if not there is not?

In reality there will always be some torque, but it will likely be smaller with clutch disengaged. Whether you model that torque is your decision.

 

[Zalajbeg]

If the equations are independent, then this indicates a problem in your assumptions, about which values can be freely chosen.

Is it possible to say if the equations are independent or not easily or do I need to find it mathematically (e.g calculating the rank of the coeffecient matrix)

In reality there will always be some torque, but it will likely be smaller with clutch disengaged. Whether you model that torque is your decision.

Let us say I want to model this, unknown, small torque too. For both of the situations (clutch engaged and clutch not engaged) I need to define a torque and the equations are the same for both of the situations. As all of the unknowns and equations are the same how can I expect to get a different torque value? What must be different in the equations or unknowns?

I have thought a bit and it seems the different states may prevent me some other assumptations (May be I cannot ignore the torque in the rear wheel if I care clutch is disengaged or not etc.) and this will bring some other unknowns and they cannot be freely chosen, Therefore I may need to assign experimentally values to some unknowns and this will bring different boundary conditions. I think this can show the difference.

As my main investigation is about the temperature distribution I will not take the clutch situation into my model (I think it will not make a big difference, if the clutch is disengaged the torque must deccelerate until the transmission, otherwise it will affect also the pistons etc.)

Though it would be good to hear your advises. Thanks for all your help!

 

[Zalajbeg]

If the equations are independent, then this indicates a problem in your assumptions, about which values can be freely chosen.In reality there will always be some torque, but it will likely be smaller with clutch disengaged. Whether you model that torque is your decision.

Today, I made two calculations with the above equations with the corrections regarding the discussion here. The bad thing is that the acceleration and most of the forces are found equal to zero. I checked the results with the original equations and the results satisfy.

The equations I used are (Also I tried wth no torque on the rear wheel):

I didn't show the vertical forces,the only equation they can be shown is the equation 2 but they cancel each other there. Could you please advise me a model which will not give me the acceleration value zero?

 

[A.T.]

Today, I made two calculations with the above equations with the corrections regarding the discussion here.

You didn't correct equation 2 now 1.

 

[Zalajbeg]

Sorry for sendind a wrong picture,

In my calculations I used the corrected form:

[itex]F_{a,1}-F_{a,2}-F=(M-2m).a[/itex]

However the result for the acceleration is always "zero". I can send the operations and the matrices (Gauss Elemination) tomorrow if you want to see. The only unknowns not equal to zero are the torque and the axle reaction force on the front wheel and they cancel the braking force.

 

[A.T.]

I didn't show the vertical forces,the only equation they can be shown is the equation 2 but they cancel each other there.

How do you know the vertical forces from the wheels on the chassis produce no net torque?

 

[Zalajbeg]

Let us say the horizontal distance between the CM of the vehicle and the center of the front wheel is L₁. And the distance between the centers of the wheels is L. The vertical reaction forces are N₁ for the front wheel and N₂ for the rear wheel.

First of all I am taking whole vehicle as the free body. The torque on the contact point (road and the weel) of the front wheel (which is zero as the vehicle is not rotating) is:

[itex]W.L_1-N_2.L=0[/itex] (***)

The friction forces (the only external horizontal forces) produce no torque as the point is on their direction.

After that I am taking the wheels as bodies. The vertical forces are: F_a,v (the vertical force from the chasis to wheel), mg (the weight of the wheel) and N (the reaction force from the ground). As there is no vertical acceleration F_a,v=N-mg. This is also the magnitude of the vertical force from wheel to chasis.

Now I am taking the vehicle without wheels as the body. The equation 2 on the pictures is the torque on the center of the front wheel.

[itex]T_{a,1}-T_{a,2}=F.r_f+(N_2-mg).L-W.L_1[/itex]

From the equation (***)

[itex]T_{a,1}-T_{a,2}=F.r_f+N_2.L-mgL-W.L_1[/itex]
[itex]T_{a,1}-T_{a,2}=F.r_f-mgL[/itex]

In fact I didn't take this mgL term into consideration. I have updated my calculations with this, the acceleration is not "zero" anymore but it is again independent of the brake force F. It doesn't seem logical as it would mean the vehicle will deccelerate even I do not press the brake pedal.

My calculations are in the attached file. (Most of them is Gauss Elimination).

 

[rcgldr]

If only the front wheels are braking, then as the vehicle slows, the torque on the rear tires equal the angular inertia of the rear tires times the rate of angular decleration, which corresponds to a backwards force applied by the rear tires to the pavement and a forward force applied by the pavement to the rear tires (this force times the radius equals the torque related to the angular deceleration of the rear wheels). You can imagine that the greater the amount of angular inertia in the rear tires, the greater the amount of braking force applied to the front tires required in order to slow the vehicle down at the same rate of deceleration.

 

[Zalajbeg]

If only the front wheels are braking, then as the vehicle slows, the torque on the rear tires equal the angular inertia of the rear tires times the rate of angular decleration, which corresponds to a backwards force applied by the rear tires to the pavement and a forward force applied by the pavement to the rear tires (this force times the radius equals the torque related to the angular deceleration of the rear wheels). You can imagine that the greater the amount of angular inertia in the rear tires, the greater the amount of braking force applied to the front tires required in order to slow the vehicle down at the same rate of deceleration.

I agree, I don't think the deccelaration is independent of the force. However I cannot find what is wrong with my model, my calculations contradicts with the reality and I need a model for braking.

 

[A.T.]

First of all I am taking whole vehicle as the free body...

After that I am taking the wheels as bodies ...Now I am taking the vehicle without wheels as the body.

Mixing up different cuts creates redundant equations

 

[Zalajbeg]

Mixing up different cuts creates redundant equations

I have noticed that I may be choosing the point for moment calculations wrong. If an object is in static equilibrum the point can be choosen arbitrary but isn't it the case for the dynamics?

Let us say there is a stick with the length of L. Two forces (F) perpendicular to this stick pulls it from the two end. I can say that the stick will have only a transitional acceleration but it will not rotate. If I calculate the moment regarding the center of the stick it shows the net torque is 0. However if I calculate a moment regarding one end there is a torque of F.L

Is it a rule about the point the net torque must be calculated regarding?

 

[A.T.]

I have noticed that I may be choosing the point for moment calculations wrong.

That's not the point. You are combining equations based on the whole car with those based on it's parts. Those equations might not be independent, because the car is just the sum of its parts, so the whole car equation might just be the sum of several car part equations.

 

[Zalajbeg]

That's not the point. You are combining equations based on the whole car with those based on it's parts. Those equations might not be independent, because the car is just the sum of its parts, so the whole car equation might just be the sum of several car part equations.

I agree with that. I am going to use only the equations for the parts. At my first try I have seen the equations from the whole car are not independent. However I just want to make sure that I use the equations for the parts correctly.

Could you please answer the question about the forces pulling a stick. After that I will do my calculations again without using the whole vehicle equations.