- #1
tuttyfruitty
- 10
- 0
I'm trying to determine the frequency of this oscillator . The traditional resonant frequency equation for the tank circuit doesn't give the correct answer as the feed back capacitor effects the circuit .
i would also like to know what the feedback capacitor does? any help would be great.
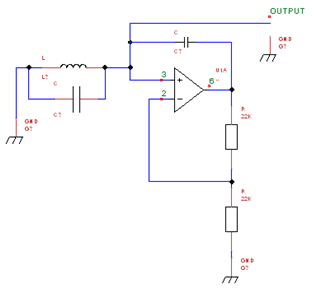
i would also like to know what the feedback capacitor does? any help would be great.