- #1
Pushoam
- 962
- 52
Homework Statement
Homework Equations
The Attempt at a Solution
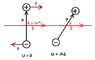
In case of uniform E, torque ##\vec N = \vec p \times \vec E
\\ U = \int_0 ^ \theta N d \theta = pE \int_0 ^ \theta \sin \theta d \theta = - pE \cos \theta
\text { Here, I assumed that the direction of } \vec N ~ and ~ \vec d \theta ~ are ~ same .
\\ U = - \vec p \dot \vec E ##
How to show the same for non - uniform E ?