- #1
zrek
- 115
- 0
I know the fenomenon of diffraction (one slit) in case of electromagnetic waves.
http://en.wikipedia.org/wiki/Diffraction
What happens if there is only a static electric field?
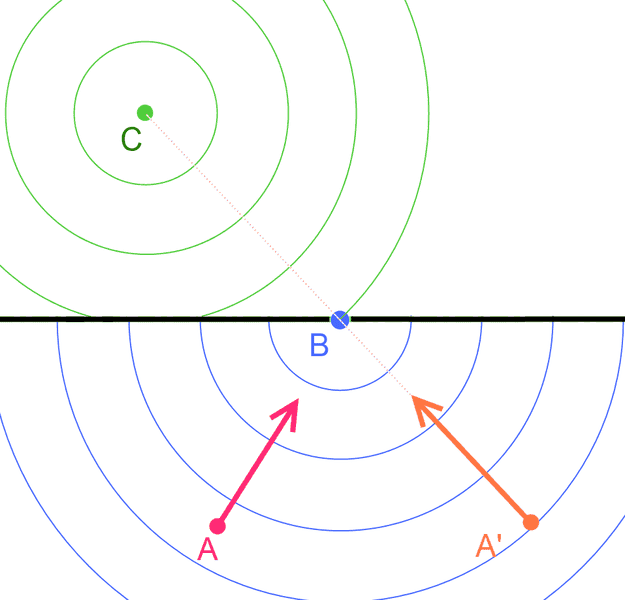
There is a point-like charge at the point C.
The black line is a wall that blocks the electric field.
At the point B there is a hole in the wall.
A and A' are test charges to measure the force, the field direction.
What we will measure?
Possible answers:
1: The picture is correct, at the point A the force directs to the hole, the point B. The test charge A will feel a force which is as big as it would come from the distance AB+BC.
2: This experiment is not possible, there is no way to block the static electric field by a wall.
3: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AB+BC.
4: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AC, just like as it would be without the wall.
5: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, as it is on the picture, as big as it would feel without the wall.
6: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, but a weaker one than it would be without the wall.
7: Other possibilities?
What do you think, which is the correct answer?
Thank you!
http://en.wikipedia.org/wiki/Diffraction
What happens if there is only a static electric field?
There is a point-like charge at the point C.
The black line is a wall that blocks the electric field.
At the point B there is a hole in the wall.
A and A' are test charges to measure the force, the field direction.
What we will measure?
Possible answers:
1: The picture is correct, at the point A the force directs to the hole, the point B. The test charge A will feel a force which is as big as it would come from the distance AB+BC.
2: This experiment is not possible, there is no way to block the static electric field by a wall.
3: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AB+BC.
4: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AC, just like as it would be without the wall.
5: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, as it is on the picture, as big as it would feel without the wall.
6: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, but a weaker one than it would be without the wall.
7: Other possibilities?
What do you think, which is the correct answer?
Thank you!