- #1
kidsasd987
- 143
- 4
https://www.particleincell.com/2012/curvilinear-coordinates/
http://www.jfoadi.me.uk/documents/lecture_mathphys2_05.pdf
Hi, I have a question about the curvilineare coordinate system.
I wonder why
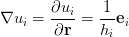 is normal to the isosurfaces?isnt ei a tangent vector to the surface ui
is normal to the isosurfaces?isnt ei a tangent vector to the surface ui
since
"With these definitions, we can define the unit vector in the
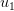 direction (basis vector)"
direction (basis vector)"
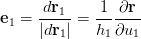
http://www.jfoadi.me.uk/documents/lecture_mathphys2_05.pdf
Hi, I have a question about the curvilineare coordinate system.
I wonder why
since
"With these definitions, we can define the unit vector in the