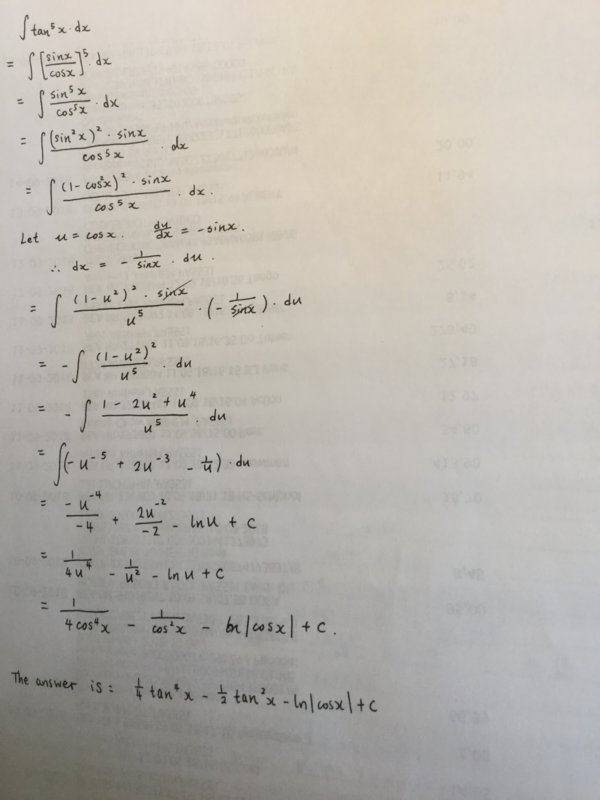- #1
youmei0426
- 18
- 0
- Homework Statement
- find the integration of (tanx)^5
- Relevant Equations
- -
This is my working out, and I also included the correct answer in the last line. The answer used a different method, however, what did I do wrong with my method? Thanks for the help!