Coordinates of Pushforwards .... General Case

[Math Amateur]

I am reading John M. Lee's book: Introduction to Smooth Manifolds ...

I am focused on Chapter 3: Tangent Vectors ...

I need some help in fully understanding Lee's conversation on computations with tangent vectors and pushforwards ... in particular I need help with a further aspect of Lee's exposition of pushforwards in coordinates concerning a map [itex]F: M \longrightarrow N[/itex] between smooth manifolds [itex]M[/itex] and [itex]N[/itex] ... ...

The relevant conversation in Lee is as follows:

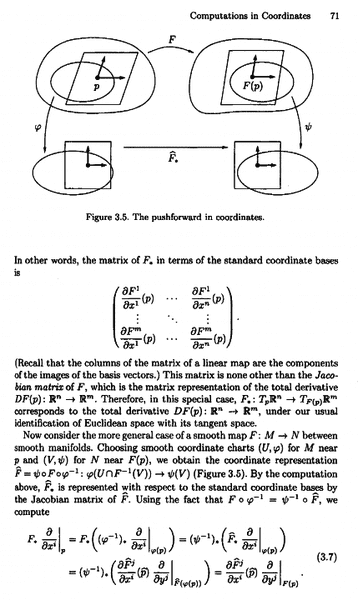
In the above text, equation 3.7 reads as follows:

" ... ...

[itex]F_* \frac{ \partial }{ \partial x^i } |_p = F_* ( ( \phi^{-1} )_* \ \frac{ \partial }{ \partial x^i } |_{\phi(p)}) [/itex][itex]= ( \psi^{-1} )_* \ ( \tilde{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)} )[/itex][itex]= ( \psi^{-1}_* ) ( \frac{ \partial \tilde{F}^j }{ \partial x^i } ( \tilde{p}) \frac{ \partial }{ \partial y^j }|_{ \tilde{F} ( \phi (p))} )[/itex][itex]= \frac{ \partial \tilde{F}^j }{ \partial x^i } ( \tilde{p} ) \frac{ \partial }{ \partial y^j }|_{ F (p) }[/itex]... ... ... ... ... 3.7

... ... ... "
I cannot see how Equation 3.7 is derived ... can someone please help ...
Specifically, my questions are as follows:Question 1

What is the explicit logic and justification for the step

[itex]F_* ( ( \phi^{-1} )_* \ \frac{ \partial }{ \partial x^i } |_{\phi(p)})[/itex] [itex]= ( \psi^{-1} )_* \ ( \tilde{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)} )[/itex]
Question 2

What is the explicit logic and justification for the step[itex]= ( \psi^{-1} )_* \ ( \tilde{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)} )[/itex][itex]= ( \psi^{-1}_* ) ( \frac{ \partial \tilde{F}^j }{ \partial x^i } ( \tilde{p}) \frac{ \partial }{ \partial y^j }|_{ \tilde{F} ( \phi (p))} )[/itex]
Question 3

What is the explicit logic and justification for the step

[itex] ( \psi^{-1}_* ) ( \frac{ \partial \tilde{F}^j }{ \partial x^i } ( \tilde{p}) \frac{ \partial }{ \partial y^j }|_{ \tilde{F} ( \phi (p))} )[/itex][itex]= \frac{ \partial \tilde{F}^j }{ \partial x^i } ( \tilde{p} ) \frac{ \partial }{ \partial y^j }|_{ F (p) }[/itex]
As you can see ... I am more than slightly confused by equation 3.7 ... hope someone can help ...Peter

===========================================================

To give readers the notation and context for the above I am providing the text of Lee's section on Computations in Coordinates (pages 69 -72) ... ... as follows:

 

[andrewkirk]

Question 1

What is the explicit logic and justification for the step

[itex]F_* ( ( \phi^{-1} )_* \ \frac{ \partial }{ \partial x^i } |_{\phi(p)})[/itex][itex]= ( \psi^{-1} )_* \ ( \tilde{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)} )[/itex]

Applying ##\psi^{-1}## to both sides of the definition of ##\hat F## we get
$$\psi^{-1}\circ\hat F=\psi^{-1}\circ\psi\circ F\circ\phi^{-1}=
F\circ\phi^{-1}$$
We then use the property of pushforwards ##(A\circ B)_*=A_*\circ B_*## to obtain
$$\psi^{-1}{}_*\circ\hat F_*=\psi^{-1}{}_*\circ\psi\circ F_*\circ\phi^{-1}{}_*=
F_*\circ\phi^{-1}{}_*$$

Applying both sides of this to ##\frac{ \partial }{ \partial x^i }|_{\phi(p)} ## and using the associative law for function composition, we get the result.

 

[andrewkirk]

Lee is correct - this part of the topic is 'hopelessly abstract'. I suppose it becomes easier with practice.
Anyway, here's my stab at the second question.

Question 2

What is the explicit logic and justification for the step[itex]= ( \psi^{-1} )_* \ ( \hat{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)} )= ( \psi^{-1}_* ) ( \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} ( \phi (p))} )[/itex]

First let's get rid of the ##\psi^{-1}{}_*##. If we can show the insides of the parentheses are the same then it follows that after applying ##\psi^{-1}## they'll remain the same.

So we want to convince ourselves that
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} ( \phi (p))} $$
Next let's remove the confusion arising from multiple names for the same thing by replacing ##\phi(p)## by ##\hat p##, to get
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\hat p}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} (\hat p)} $$
Note that this equation is now just about a map ##\hat F## from ##\mathbb{R}^n## to ##\mathbb{ R}^m##. That is, it's just a formula in multivariable calculus, with no need to consider general manifolds.
Let's replace ##\hat F## by ##G## and ##\hat p## by ##\vec x## to make that clearer. Also, since ## \frac{ \partial }{ \partial x^i } |_{\hat p}## and ##\frac{ \partial }{ \partial y^j }|_{ \hat{F} (\hat p)}## in their respective contexts in this equation are basis vectors for ##\mathbb R^n## and ##\mathbb R^m## respectively, let's use a simpler notation to denote them as ##\vec e_i^{(n)}## and ##\vec e_j^{(m)}##.

So we write
$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$

This is now just the familiar result from multivariable calculus, that the differential ##G_*## of a map ##G:\mathbb{R}^n\to\mathbb{R}^m##, applied to a basis vector of ##\mathbb R^n## is equal to the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##.

So all this step in question 2 is doing is writing the image of ##\hat F{}_*## applied to a basis vector of ##\mathbb R^n## in terms of Jacobian entries and basis vectors in ##\mathbb R^m##.

But we had to cut through quite a bit of abstract notation to get to that.

 

[andrewkirk]

Question 3 is easier.

We want to justify

$$ \psi^{-1}_* \left( \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }\Big|_{ \hat{F} ( \phi (p))} \right)
= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p} ) \frac{ \partial }{ \partial y^j }\Big|_{ F (p) }
$$

Proceed as follows
\begin{align*}
\psi^{-1}{}_* \left( \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }\Big|_{ \hat{F} ( \phi (p))} \right)
&=\frac{ \partial \hat{F}^j }{ \partial x^i }( \hat{p})\ \psi^{-1}{}_* \left( \frac{ \partial }{ \partial y^j }\Big|_{ \hat{F} ( \phi (p))} \right) \\
&=\frac{ \partial \hat{F}^j }{ \partial x^i }( \hat{p})\ \left(\psi^{-1}{}_* \left( \frac{ \partial }{ \partial y^j }\Big|_{ \psi(F(p))} \right) \right)\\
&=\frac{ \partial \hat{F}^j }{ \partial x^i }( \hat{p})\
\frac{ \partial }{ \partial y^j }\Big|_{ F(p)}\\
\end{align*}
The first equality follows from linearity of ##\psi^{-1}{}_*##, the second from the definition of ##\hat F## and the third from Lee's definition in the first equation after the heading 'Computations in Coordinates', but this time applied to the pair of spaces ##N,\psi(N)## rather than ##M,\phi(M)##.

 

[Math Amateur]

Andrew ... thanks for your substantial help ... I really appreciate your support for my attempt to understand these notions ...

I have nearly given up trying to understand the topic, so your help is very timely ...

Just working through your posts in detail now ...

Thanks again,

PeterPS Wish there were some computational examples involving these theoretical notions ...

 

[Math Amateur]

Lee is correct - this part of the topic is 'hopelessly abstract'. I suppose it becomes easier with practice.
Anyway, here's my stab at the second question.

First let's get rid of the ##\psi^{-1}{}_*##. If we can show the insides of the parentheses are the same then it follows that after applying ##\phi^{-1}## they'll remain the same.

So we want to convince ourselves that
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} ( \phi (p))} $$
Next let's remove the confusion arising from multiple names for the same thing by replacing ##\phi(p)## by ##\hat p##, to get
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\hat p}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} (\hat p)} $$
Note that this equation is now just about a map ##\hat F## from ##\mathbb{R}^n## to ##\mathbb{ R}^m##. That is, it's just a formula in multivariable calculus, with no need to consider general manifolds.
Let's replace ##\hat F## by ##G## and ##\hat p## by ##\vec x## to make that clearer. Also, since ## \frac{ \partial }{ \partial x^i } |_{\hat p}## and ##\frac{ \partial }{ \partial y^j }## in their respective contexts in this equation are basis vectors for ##\mathbb R^n## and ##\mathbb R^m## respectively, let's use a simpler notation to denote them as ##\vec e_i^{(n)}## and ##\vec e_j^{(m)}##.

So we write
$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$

This is now just the familiar result from multivariable calculus, that the differential ##G_*## of a map ##G:\mathbb{R}^n\to\mathbb{R}^m##, applied to a basis vector of ##\mathbb R^n## is equal to the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##.

So all this step in question 2 is doing is writing the image of ##\hat F{}_*## applied to a basis vector of ##\mathbb R^n## in terms of Jacobian entries and basis vectors in ##\mathbb R^m##.

But we had to cut through quite a bit of abstract notation to get to that.

Hi Andrew ... I need a little further help on a basic point ...

In your post above you write:
" ... ...So we write

$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$

This is now just the familiar result from multivariable calculus, that the differential ##G_*## of a map ##G:\mathbb{R}^n\to\mathbb{R}^m##, applied to a basis vector of ##\mathbb R^n## is equal to the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##. ... ... "
BUT ... I cannot quite see how this standard result works out ...To indicate the way I think it goes (there must be a mistake in my viewpoint!) ... consider an example ...Say that [itex] G(x_1, x_2) = (3x_1 + x_2^2 , x_1 cos x_2 , e^{ x_1 - 2 x_2} ) [/itex]

then the differential [itex] G_* = dG[/itex] at [itex] \vec{e}_1 = (1,0) [/itex] is determined as follows:[itex]dG (\vec{e}_1) [/itex][itex]= dG ( \ (1,0) \ ) [/itex]= [itex] \begin{pmatrix} \frac{ \partial G_1 }{ \partial x_1} & \frac{ \partial G_1}{ \partial x_2} \\ \frac{ \partial G_2}{ \partial x_1} & \frac{ \partial G_2}{ \partial x_2} \\ \frac{ \partial G_3}{ \partial x_1} & \frac{ \partial G_3}{ \partial x_2} \end{pmatrix}_{ ( \vec{e}_1 ) } [/itex]
= [itex] \begin{pmatrix} 3 & 2 x_2 \\ cos \ x_2 & - x_1 sin \ x_2 \\ e^{ x_1 - 2 x_2} & -2 e^{ x_1 - 2 x_2} +2 \end{pmatrix}_{ ( 1, 0 ) } [/itex]
Now evaluating at (1,0) we get[itex]dG (\vec{e}_1) [/itex] = [itex] \begin{pmatrix} 3 & 2.0 \\ cos \ 0 & - 1 sin \ 0 \\ e^{ 1 - 2 .0} & -2 e^{ 1 - 2. 0} +2 \end{pmatrix}_{ ( 1, 0 ) } [/itex][itex]dG (\vec{e}_1) [/itex] = [itex] \begin{pmatrix} 3 & 0 \\ 1 & 0 \\ e & -2 e +2 \end{pmatrix} [/itex]Now this obviously does not equal the sum over j of the relevant column of the Jacobian of G ... obviously my procedure is wrong ... but why ...

How should I be approaching this matter ... ? ... ...

... so the substance of my question is how ... exactly (including the mechanics) ... do we 'apply' the differential [itex] dG = G_* [/itex] to a basis vector of [itex] \mathbb{R}^n [/itex] and get the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##. ... ... ?

Can you help and clarify this situation ...

Peter

 

[fresh_42]

$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$
Say that [itex] G(x_1, x_2) = (3x_1 + x_2^2 , x_1 cos x_2 , e^{ x_1 - 2 x_2} ) [/itex]

I get ##G_* (\vec e_1) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_1} (\vec x) \vec e_j = 3 \cdot \vec e_1 + \cos x_2 \cdot \vec e_2 + e^{x_1-2x_2} \cdot \vec e_3##

and ##G_* (\vec e_2) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_2} (\vec x) \vec e_j = 2x_2 \cdot \vec e_1 - x_1 \sin x_2 \cdot \vec e_2 - 2e^{x_1-2x_2} \cdot \vec e_3.##

Now we can evaluate at whatever point we want to.
At ##(1,0)## I get ##G_* = (dG_1,dG_2) = \begin{pmatrix} 3 & 0 \\ 1 & 0 \\ e & -2 e \end{pmatrix}.##

 

[Math Amateur]

Lee is correct - this part of the topic is 'hopelessly abstract'. I suppose it becomes easier with practice.
Anyway, here's my stab at the second question.

First let's get rid of the ##\psi^{-1}{}_*##. If we can show the insides of the parentheses are the same then it follows that after applying ##\phi^{-1}## they'll remain the same.

So we want to convince ourselves that
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\phi(p)}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} ( \phi (p))} $$
Next let's remove the confusion arising from multiple names for the same thing by replacing ##\phi(p)## by ##\hat p##, to get
$$\hat{F}_* \frac{ \partial }{ \partial x^i } |_{\hat p}= \frac{ \partial \hat{F}^j }{ \partial x^i } ( \hat{p}) \frac{ \partial }{ \partial y^j }|_{ \hat{F} (\hat p)} $$
Note that this equation is now just about a map ##\hat F## from ##\mathbb{R}^n## to ##\mathbb{ R}^m##. That is, it's just a formula in multivariable calculus, with no need to consider general manifolds.
Let's replace ##\hat F## by ##G## and ##\hat p## by ##\vec x## to make that clearer. Also, since ## \frac{ \partial }{ \partial x^i } |_{\hat p}## and ##\frac{ \partial }{ \partial y^j }## in their respective contexts in this equation are basis vectors for ##\mathbb R^n## and ##\mathbb R^m## respectively, let's use a simpler notation to denote them as ##\vec e_i^{(n)}## and ##\vec e_j^{(m)}##.

So we write
$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$

This is now just the familiar result from multivariable calculus, that the differential ##G_*## of a map ##G:\mathbb{R}^n\to\mathbb{R}^m##, applied to a basis vector of ##\mathbb R^n## is equal to the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##.

So all this step in question 2 is doing is writing the image of ##\hat F{}_*## applied to a basis vector of ##\mathbb R^n## in terms of Jacobian entries and basis vectors in ##\mathbb R^m##.

But we had to cut through quite a bit of abstract notation to get to that.

I get ##G_* (\vec e_1) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_1} (\vec x) \vec e_j = 3 \cdot \vec e_1 + \cos x_2 \cdot \vec e_2 + e^{x_1-2x_2} \cdot \vec e_3##

and ##G_* (\vec e_2) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_2} (\vec x) \vec e_j = 2x_2 \cdot \vec e_1 - x_1 \sin x_2 \cdot \vec e_2 - 2e^{x_1-2x_2} \cdot \vec e_3.##

Now we can evaluate at whatever point we want to.
At ##(1,0)## I get ##G_* = (dG_1,dG_2) = \begin{pmatrix} 3 & 0 \\ 1 & 0 \\ e & -2 e \end{pmatrix}.##

I get ##G_* (\vec e_1) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_1} (\vec x) \vec e_j = 3 \cdot \vec e_1 + \cos x_2 \cdot \vec e_2 + e^{x_1-2x_2} \cdot \vec e_3##

and ##G_* (\vec e_2) = \sum_{j=1}^{3} \frac{\partial G_j}{\partial x_2} (\vec x) \vec e_j = 2x_2 \cdot \vec e_1 - x_1 \sin x_2 \cdot \vec e_2 - 2e^{x_1-2x_2} \cdot \vec e_3.##

Now we can evaluate at whatever point we want to.
At ##(1,0)## I get ##G_* = (dG_1,dG_2) = \begin{pmatrix} 3 & 0 \\ 1 & 0 \\ e & -2 e \end{pmatrix}.##

Thanks fresh-42 ...

I do not think you have answered my problem ... but then maybe I did not make myself clear ...

Basically I am perplexed at Andrew's statement that the differential ##G_*## of a map ##G:\mathbb{R}^n\to\mathbb{R}^m##, applied to a basis vector of ##\mathbb R^n## is equal to the sum (over ##j##) of the relevant column of the Jacobian matrix multiplied by the basis vectors of ##\mathbb{R}^m##. ... so I showed what I thought was the differential [itex] G_* \equiv dG [/itex] of a map that I defined evaluated or 'applied' at the basis vector [itex] \vec{e}_1 = (1, 0) [/itex] ... basically my procedure resulted in a matrix ... NOT the sum of terms that you got quite correctly from applying Andrew's (or Lee's) formula ... so I think that I am not actually "applying" the differential to a basis vector in the sense Andrew means ...

So ... I am trying to understand how the formula

$$G_*\left( \vec e_i^{(n)} \right)= \frac{ \partial G^j }{ \partial x^i } ( \vec{x}) \vec e_j^{(m)}$$

is exactly the same as what I understand as applying/evaluating the differential at/to a basis vector ...

What I understand by applying or evaluating a differential at a basis vector is illustrated by my evaluation of the differential in my example at the basis vector [itex] \vec{e}_1 = (1, 0) [/itex] ... BUT I am clearly not following the procedure that gives you a sum of terms like Andrew's formula ... because as you saw from my example all I got was a matrix ...

Hope I have clarified my problem ... ( but maybe I haven't )

Let me know if I have not made myself clear ...

Peter

 

[fresh_42]

To be honest: not really.
The ##\vec e_i## are basis vectors. ##G_*## is represented by the Jacobi matrix according to these vectors. If you drop them you get coordinates arranged as vectors.

I have the feeling that you don't distinguish between the point at which the direction is measured and the direction itself. Remember the discussion in which Andrew explained that it is actually ##p + T_p(M)## to consider, the point of evaluation plus the direction of the tangent vectors.

At ##(0,0)## the tangent space is spanned by ##(3,1,1)## and ##(0,0,-2)## wrt to the canonical basis. If you evaluate the derivative at ##(1,0)## you get the tangent space spanned by ##(3,1,e)## and ##(0,0,-2e)## wrt to the canonical basis, at ##(0,1)## by ##\{(3,\cos 1,e^{-2}),(2,0,-2e^{-2})\}.##
Thus you see that the tangent space (a plane in ##ℝ^3##) varies as you change position on the manifold (defined by ##G##).

 

[Math Amateur]

Hi fresh_42,

After some reading and reflection I realized you were right on the money in diagnosing my problem ... I was not distinguishing between the point at which the direction is measured and the direction itself ... I also need to realize that the differential or total derivative was a linear map between [itex] \mathbb{R}^n [/itex] and [itex]\mathbb{R}^m [/itex] and so operates on or transforms a vector in [itex] \mathbb{R}^n [/itex] to a vector in [itex] \mathbb{R}^m [/itex] ... ...

Thanks to you and Andrew for all your help ... it is much appreciated ...

Peter