Confusion about the Concept of Operators

[jdou86]

Dear all,

I've been reading and got confused of the concept below

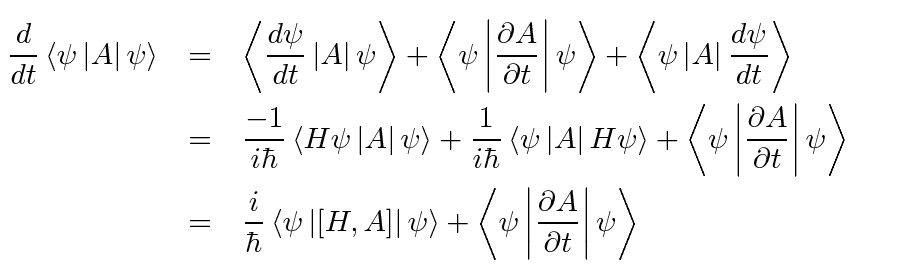
have two questions

question 1)
For <ψ|HA|ψ> = <Hψ|A|ψ>, why does the Hamiltonian operator acting on the bra state
and <ψ|AH|ψ> in this configuration it will act on the ket state?

question 2)
what does it mean for H|ψ> = |Hψ> did the state change? or it's simply a constant, (it can't be right since if so any operator will commute with Hamiltonian)

Thank you.

Jon

 

[PeterDonis]

I've been reading

What source have you been reading? Please give a reference. It's a lot easier to help if we have the context of where you are getting information from.

 

[jdou86]

What source have you been reading? Please give a reference. It's a lot easier to help if we have the context of where you are getting information from.

https://quantummechanics.ucsd.edu/ph130a/130_notes/node189.html

 

[PeterDonis]

Ok, looking at your source it seems like it's just being rather cavalier with notation. In the casual notation this source is using, the ket ##|H \psi \rangle## just means "the ket you get by operating on ##| \psi \rangle## with ##H## from the left", i.e., ##H | \psi \rangle = | H \psi \rangle## is just a definition of how they're using notation and tells you nothing about any physics. Similarly, the bra ##\langle H \psi |## just means "the bra you get by operating on ##\langle \psi |## with ##H## from the right", i.e., ##\langle \psi | H = \langle H \psi |## is just a definition of their notation. (In the latter case the notation is particularly confusing since the operator is operating from the right, but it appears on the left inside the bra.)

 

[jdou86]

Ok, looking at your source it seems like it's just being rather cavalier with notation. In the casual notation this source is using, the ket ##|H \psi \rangle## just means "the ket you get by operating on ##| \psi \rangle## with ##H## from the left", i.e., ##H | \psi \rangle = | H \psi \rangle## is just a definition of how they're using notation and tells you nothing about any physics. Similarly, the bra ##\langle H \psi |## just means "the bra you get by operating on ##\langle \psi |## with ##H## from the right", i.e., ##\langle \psi | H = \langle H \psi |## is just a definition of their notation. (In the latter case the notation is particularly confusing since the operator is operating from the right, but it appears on the left inside the bra.)

yeah but isn't H|ψ> = E |ψ(>*edit) commutator cancels out?

 

[PeterDonis]

isnt H|ψ> = E |ψ(>*edit)

Only if the system is in an eigenstate of ##H##.

 

[jdou86]

Could it still be true if it's under Dirac formalism? I'm kinda confused because if you can do change of basis diagonalizing hamiltonian then change to the new orthogonal eigenbasis. Then you will always have E as their eigenvalues.

Maybe I'm totally lost.

 

[vanhees71]

It's of course the usual Dirac bra-ket notation, and there's nothing mysterious about it. One should also note that everything is in the Schrödinger picture of time evolution, i.e., the states carry the entire time dependence, while the fundamental operators for observables are time-independent. Now ##\hat{A}## is an operator that is in addition also explicitly time dependent. In the Schrödinger picture you have
$$\mathrm{i} \partial_t |\psi(t) \rangle = \hat{H} |\psi(t) \rangle,$$
where ##\hat{H}## (which may be explicitly time dependent or not) is the Hamilton operator, which must be self-adjoint.

Taking the adjoint of this equation, you get
$$-\mathrm{i} \partial_t \langle \psi(t)| = \langle \psi(t)| \hat{H}^{\dagger} = \langle \psi(t)| \hat{H} = \langle \hat{H} \psi(t)|.$$
Finally you have
$$\frac{\mathrm{d}}{\mathrm{d} t} \hat{A}=\partial_t \hat{A},$$
i.e., the time derivative refers only to a possible explicit time dependence.

Now you should easily understand the copied calculation from your textbook by using the rule for product differentiation and the just derived formulae above.

 

[PeterDonis]

Could it still be true if it's under Dirac formalism?

Could what still be true?

I'm kinda confused because if you can do change of basis diagonalizing hamiltonian then change to the new orthogonal eigenbasis. Then you will always have E as their eigenvalues.

Yes, you are confused. Whether or not a particular state ##| \psi \rangle## is an eigenstate of the Hamiltonian ##H## has nothing to do with what basis you write the states in. The eigenvalue equation ##H | \psi \rangle = E | \psi \rangle## is only satisfied by states ##| \psi \rangle## that are eigenstates of ##H##; that equation is basis independent (a state that satisfies it does so in any basis). But most states are not eigenstates of ##H##, so they don't satisfy that equation.

 

[jdou86]

Either system (ket) state or Hamiltonian which ever you wan to call it can be radiagonalized to be the eigenstates.

Think I got it now operators can act on each other just like some off diagonal matrices

 

[PeterDonis]

Either system (ket) state or Hamiltonian which ever you wan to call it can be radiagonalized to be the eigenstates.

Diagonalization does not affect which states are eigenstates. Diagonalization is just a change of basis. See my previous post.

 

[jdou86]

Diagonalization does not affect which states are eigenstates. Diagonalization is just a change of basis. See my previous post.

So why not pick a basis that contains the eigenkets of H?

 

[PeterDonis]

So why not pick a basis that contains the eigenkets of H?

You can pick whatever basis you want. What difference does it make?

 

[PeterDonis]

commutator cancels out?

Whether or not ##H## commutes with ##A## doesn't depend on what state ##| \psi \rangle## they are operating on.

 

[jdou86]

Feel like we are speaking different languages, i would stop here. Thank you, I get the logistic now. I appreciate for your time. Enjoy the rest of the sunday.

-J