Collapse of state vector for continuous eigenvalues

[bob900]

1. In the many statements of the QM postulates that I've seen, it says that if you measure an observable (such as position) with a continuous spectrum of eigenvalues, on a state such as

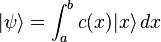
then the result will be one of the eigenvalues x, and the state vector will collapse to the eigenvector |x>.

However, for say the position operator, the eigenvectors are the dirac delta functions δ(x-x') and they do not represent physically realizable states (since they can't be normalized). So what does the state vector actually collapse to?

2. In practice there will always be experimental uncertainty Δ due to the resolution of your measuring apparatus, etc. So if you measure some position x, with an uncertainty +/- Δ, does the state vector still collapse to an eigenvector corresponding to some particular eigenvalue within the [x-Δ, x+Δ] range? Or does it collapse perhaps to some (of infinitely many) states ψ(z) such that for z outside of the [x-Δ, x+Δ] range |ψ(z)|^2 = 0, but inside that range the probability amplitudes are equal for all z?

 

[dextercioby]

1. I'm not a supporter of the collapse proposal.
2. Point 1 of yours indeed contradicts the first axiom which excludes distributions as physical states.
3. For continuous spectrum, one tries to mend it to the other axioms and resorts to probability distributions with interval [itex] \delta [/itex] in the parameter space of the (real) continuous spectrum.

For pure states:

[tex]|\psi_{new}\rangle = \frac{P_{\delta}|\psi_{old}\rangle}{\langle \psi_{old} |P_{\delta}|\psi_{old}\rangle} [/tex]

[tex] P_{\delta} = \int_{a_{0} - \frac{\delta}{2}}^{a_{0} + \frac{\delta}{2}} d\alpha |\alpha\rangle \langle \alpha| [/tex]

 

[bob900]

2. Point 1 of yours indeed contradicts the first axiom which excludes distributions as physical states.
3. For continuous spectrum, one tries to mend it to the other axioms and resorts to probability distributions with interval [itex] \delta [/itex] in the parameter space of the (real) continuous spectrum.

For pure states:

[tex]|\psi_{new}\rangle = \frac{P_{\delta}|\psi_{old}\rangle}{\langle \psi_{old} |P_{\delta}|\psi_{old}\rangle} [/tex]

[tex] P_{\delta} = \int_{a_{0} - \frac{\delta}{2}}^{a_{0} + \frac{\delta}{2}} d\alpha |\alpha\rangle \langle \alpha| [/tex]

I think this is roughly equivalent to what a book I have (Griffiths Intro to QM) says :

"In the case of continuous spectra the collapse is to a narrow range about the measured value, depending on the precision of the measuring device".

But how do you ever know the 'precision' of your measuring device and how does it enter your practical calculations? Let's say I make your measurement device really imprecise - I measure a particle's position by having a line of very large (say 10 meter long) detector plates and recording which plate the particle strikes. That will measure position (along one direction) to the accuracy of 10 meters. Once I obtain my result and want to then calculate the evolution of the system further, I will then use, like you stated :

[tex]|\psi_{new}\rangle = \frac{P_{\delta}|\psi_{old}\rangle}{\langle \psi_{old} |P_{\delta}|\psi_{old}\rangle}[/tex]

with δ=10m, as my new initial state.

But it could be said that I have really measured it to more accuracy - perhaps there is some investigation that can be performed on the plate (looking at how its internal structure, at say the molecular level, was affected), that will allow me to find out more precisely where the particle struck, say down to the millimeter? Then I would have to use δ=10^-3m, which will produce quite different predictions than had I used δ=10m!

So it seems that for me to calculate a correct result, I would somehow have to know the maximum precision of my measuring device. How is that possible, or am I missing something basic here?

 

[strangerep]

[...] or am I missing something basic here?

Yes. But hey, don't feel bad -- everyone who uses the notion of "collapse" to try and explain QM is also missing that same "something basic"...

Get hold of Ballentine's text "QM -- A Modern Development" and study section 9.2 (and possibly some earlier chapters if sect 9.2 doesn't make sense). The basic idea is that realistic measurement involves establishing a correlation between the system's initial state and the apparatus' final state, via an interaction. The reason this emphasis is less visible in much of introductory QM material is that you can't go very far with this in general form. Rather, one must analyze each experimental situation carefully and model it appropriately. Typically, that needs a fair bit of work for every situation.