- #1
sltungle
- 27
- 0
During revision for an exam I have tomorrow I came across a question that left me confused, and I wasn't entirely satisfied with my teacher's explanation today. I'm worried something of the sort may come up in the exam and I won't be entirely certain how to deal with it.
We have a plane inclined at 15 degrees from the horizontal. The circle is 167 metres in radius. A vehicle of unknown mass is driving around this circle. We want to find out the speed that we need to have a sideways friction of 0 on the car.
The answers page has a diagram drawn up similar to this:
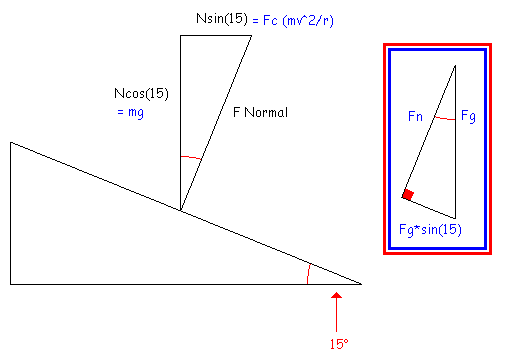
(Triangle at right hand side is the one used to determine the normal force from the gravitational force initially.)
Now this seemed all well and fine. They then divided Fc by Fg to remove mass from the equation and ended up with the equation tan(theta) = v^2/rg. Rearrange for v and you have the velocity you're looking for.
... but then I went back and pulled the problem apart and started thinking about it some more, and I got confused.
In that force triangle (the one shown in the picture at the left), the vertical component of the normal force is gravity. But... when you use the equation N = mg*cos(theta) in the first place to get the normal force we had gravity as the hypotenuse (triangle at the right); as the larger force. However, in the force triangle shown in the left of the picture the NORMAL force is the greater of the two. How does this work?
If you work your way backwards and use the equation N = mg*cos(theta) and then replace the 'N' in the vertical component with mg*cos(theta), then you end up with the vertical component in the diagram as mg*cos^2(theta), which is definitely NOT equal to mg. Yet the answer page clearly has that force labelled as 'Ncos(15) = mg'.
I'm getting really confused, and I'm getting really worried. Can somebody please help? :(
We have a plane inclined at 15 degrees from the horizontal. The circle is 167 metres in radius. A vehicle of unknown mass is driving around this circle. We want to find out the speed that we need to have a sideways friction of 0 on the car.
The answers page has a diagram drawn up similar to this:
(Triangle at right hand side is the one used to determine the normal force from the gravitational force initially.)
Now this seemed all well and fine. They then divided Fc by Fg to remove mass from the equation and ended up with the equation tan(theta) = v^2/rg. Rearrange for v and you have the velocity you're looking for.
... but then I went back and pulled the problem apart and started thinking about it some more, and I got confused.
In that force triangle (the one shown in the picture at the left), the vertical component of the normal force is gravity. But... when you use the equation N = mg*cos(theta) in the first place to get the normal force we had gravity as the hypotenuse (triangle at the right); as the larger force. However, in the force triangle shown in the left of the picture the NORMAL force is the greater of the two. How does this work?
If you work your way backwards and use the equation N = mg*cos(theta) and then replace the 'N' in the vertical component with mg*cos(theta), then you end up with the vertical component in the diagram as mg*cos^2(theta), which is definitely NOT equal to mg. Yet the answer page clearly has that force labelled as 'Ncos(15) = mg'.
I'm getting really confused, and I'm getting really worried. Can somebody please help? :(
Last edited: