Center manifold and submanifold

[jollage]

Hi all,

I am not familiar with the dynamic system theory. When I was trying to understand the weakly nonlinear stability analysis, I realize the following question.

It is known that the center manifold reduction can be used to study the first linear bifurcation. This lead to the Ginzburg-Landau equation

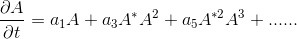
Is the center manifold corresponding to the space

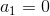? I feel this because at the linear bifurcation, the growth rate of the disturbance is zero, which implies that

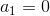in the above equation.

Then does there exist a submanifold corresponding to

?

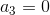Thanks a lot.

 

[pasmith]

Hi all,

I am not familiar with the dynamic system theory. When I was trying to understand the weakly nonlinear stability analysis, I realize the following question.

It is known that the center manifold reduction can be used to study the first linear bifurcation. This lead to the Ginzburg-Landau equation

Is the center manifold corresponding to the space

?

You are missing some spatial derivatives from that equation.

The centre manifold consists of the (complex) amplitudes corresponding to wavenumbers of marginally stable disturbances to some reference state of the physical quantities you are studying. Here that amplitude is [itex]A[/itex].

By adding the evolution equation for [itex]a_1[/itex], which is [itex]\frac{\partial a_1}{\partial t} = 0[/itex], we obtain the extended centre manifold, which includes the actual centre manifold as a submanifold.

[itex]a_1[/itex], [itex]a_3[/itex], and [itex]a_5[/itex] are functions of the parameters appearing in the PDE which actually governs the evolution of the physical quantities involved. At the actual bifurcation it will be the case that [itex]a_1 = 0[/itex], but the idea is that the Ginzburg-Landau equation also applies at parameter values near to, but not at, the bifurcation. For these values [itex]a_1 \neq 0[/itex].

By adding the trivial evolution equation for [itex]a_1[/itex], [itex]\frac{\partial a_1}{\partial t} = 0[/itex] to the system we obtain the extended centre manifold, which indeed contains the original centre manifold as a submanifold.

 

[jollage]

You are missing some spatial derivatives from that equation.

The centre manifold consists of the (complex) amplitudes corresponding to wavenumbers of marginally stable disturbances to some reference state of the physical quantities you are studying. Here that amplitude is [itex]A[/itex].

[itex]a_1[/itex], [itex]a_3[/itex], and [itex]a_5[/itex] are functions of the parameters appearing in the PDE which actually governs the evolution of the physical quantities involved. At the actual bifurcation it will be the case that [itex]a_1 = 0[/itex], but the idea is that the Ginzburg-Landau equation also applies at parameter values near to, but not at, the bifurcation. For these values [itex]a_1 \neq 0[/itex].

Hi pasmith,

Thanks a lot for your reply.

Yes, you are right. For the GLE, I should add some spatial-derivative terms. Here, I just listed the linear and nonlinear growth rate terms, since they are pertaining to the questions I have.

I understand what you wrote there. Do you have any clue about the existence of the submanifold for [itex]a_3 = 0[/itex]? Thanks.

 

[pasmith]

Hi pasmith,

Thanks a lot for your reply.

Yes, you are right. For the GLE, I should add some spatial-derivative terms. Here, I just listed the linear and nonlinear growth rate terms, since they are pertaining to the questions I have.

I understand what you wrote there. Do you have any clue about the existence of the submanifold for [itex]a_3 = 0[/itex]? Thanks.

It exists. We can keep extending the centre manifold by adding [itex]\frac{\partial a_n}{\partial t} = 0[/itex] to the system until we've exhausted our parameters. Fixing the value of [itex]a_n[/itex] then produces a submanifold of one fewer dimensions.

 

[jollage]

It exists. We can keep extending the centre manifold by adding [itex]\frac{\partial a_n}{\partial t} = 0[/itex] to the system until we've exhausted our parameters. Fixing the value of [itex]a_n[/itex] then produces a submanifold of one fewer dimensions.

Great, thanks. Is there any general procedure of changing the parameters to achieve this (fixing the value of [itex]a_n[/itex])? For instance, for fixing [itex]a_1=0[/itex], what I usually do is to plot a neutral curve in the parameter space, and then to choose the parameters on that neutral curve. This will guarantee that the growth rate is small. How to fix [itex]a_3[/itex] then?

Another question is that, if [itex]a_3=0[/itex] can be located in the parameter space, does it mean we can change between the subcritical and supercritical bifurcation by modifying slightly the parameters (across the curve on which [itex]a_3=0[/itex])?

Could you please tell me any reference on this subject (center manifold and submanifold)? Thanks a lot!

 

[Strum]

Perhaps somebody else have a reference? I would very much like to read it as well :)