- #1
NickTesla
- 29
- 3
I would like to understand how the Euler constant elevated to fractional exponent gave this result? 958mV someone please!?
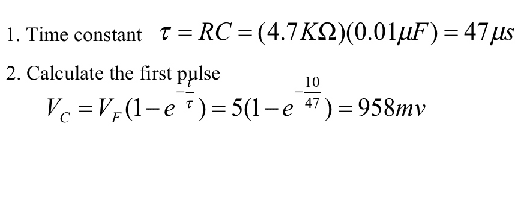
Svein said:OK. Let us take it in steps:
- [itex]\frac{10}{47}= 0.212765957 [/itex]
- [itex]e^{-0.212765957}=0.808345302 [/itex]
- [itex]1- 0.808345302=0.191655 [/itex]
- [itex]5 \cdot 0.191655 = 0.958273 [/itex]
Sven Wonderfully Thank you!Svein said:OK. Let us take it in steps:
- [itex]\frac{10}{47}= 0.212765957 [/itex]
- [itex]e^{-0.212765957}=0.808345302 [/itex]
- [itex]1- 0.808345302=0.191655 [/itex]
- [itex]5 \cdot 0.191655 = 0.958273 [/itex]
Obrigado!NickTesla said:Sven Wonderfully Thank you!












The discharge time of a capacitor can be calculated using the Euler formula, which is T = -RC ln(Vc/V0), where T is the discharge time in seconds, R is the resistance in ohms, C is the capacitance in farads, Vc is the final voltage across the capacitor, and V0 is the initial voltage across the capacitor.
The Euler formula is a mathematical equation that relates the discharge time of a capacitor to its resistance, capacitance, and initial and final voltages. It is important because it allows us to calculate the discharge time of a capacitor without having to rely on experimental data, which can be time-consuming and costly.
Yes, the Euler formula can be used for all types of capacitors, as long as the values for resistance, capacitance, and initial and final voltages are known. However, it is worth noting that this formula is most accurate for ideal capacitors, which have no internal resistance or leakage. Real-world capacitors may have slightly different discharge times due to these factors.
Yes, the discharge time of a capacitor is affected by the voltage across it. The higher the initial voltage, the longer it will take for the capacitor to fully discharge. This is because the higher voltage means more charge needs to be dissipated, which takes longer.
The Euler formula is a good approximation for calculating capacitor discharge time, but it does have some limitations. It assumes that the capacitor is discharged through a resistor, and that the voltage across the capacitor decays exponentially. In reality, there may be other components or factors at play that can affect the discharge behavior of a capacitor, so the calculated discharge time may not be 100% accurate.