- #1
Youyang Zhao
- 2
- 0
It is in the IB textbook. Said as an application of the uncertainty principle, consider an electron, which is known to be confined in a region of size L.
We know the uncertainty in position of the electron must satisfy Δx<L.
Therefore, according to the uncertainty principle, we can work out the approximate value of the uncertainty in momentum.
Then, as shown in the picture attached, an approximate value of the kinetic energy of the electron is worked out.
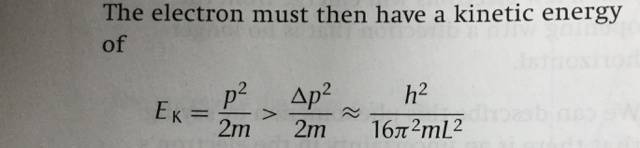
I can not understand the process. How did they work out the value of kinetic energy (or value of the momentum) with the uncertainty of the momentum?
Asking questions for the first time. Thank you for your time and patience.
We know the uncertainty in position of the electron must satisfy Δx<L.
Therefore, according to the uncertainty principle, we can work out the approximate value of the uncertainty in momentum.
Then, as shown in the picture attached, an approximate value of the kinetic energy of the electron is worked out.
I can not understand the process. How did they work out the value of kinetic energy (or value of the momentum) with the uncertainty of the momentum?
Asking questions for the first time. Thank you for your time and patience.