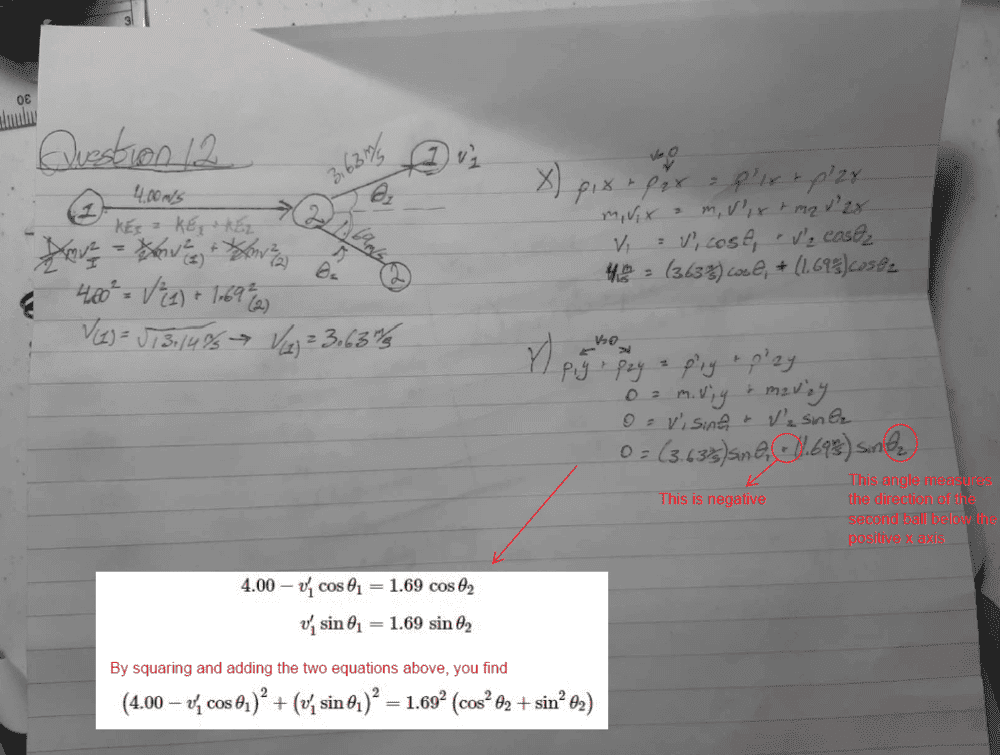- #1
ejantz
- 5
- 0
- Homework Statement
- A billiard ball moves at a speed of 4.00m/s and collides elastically with an identical stationary ball. As a result, the stationary ball flies away at a speed of 1.69m/s, as shown in Figure A2.12. Determine the final speed and direction of the incoming ball after the collision and the direction of the stationary ball after the collision
- Relevant Equations
- KEi = KE1 + KE2
p1x + p2x = p'1x + p'2x
p1y + p2y = p'1y + p'2y
cos(theta1)^2 + sin(theta1)^2 = cos(theta2)^2 + sin(theta2)^2
I know this question has been asked before but I really need some help finishing this final piece of the puzzle.. I have attached an image of my work to show how far I have gotten towards the solution but my unfamiliarity with trigonometry equations has gotten my stuck. Please assist! thank you