2D Cartesian Laplace equation with a single point diffusion

[maistral]

Hi. I have this problem in trying to solve this PDE analytically.

The PDE is represented by this diagram:

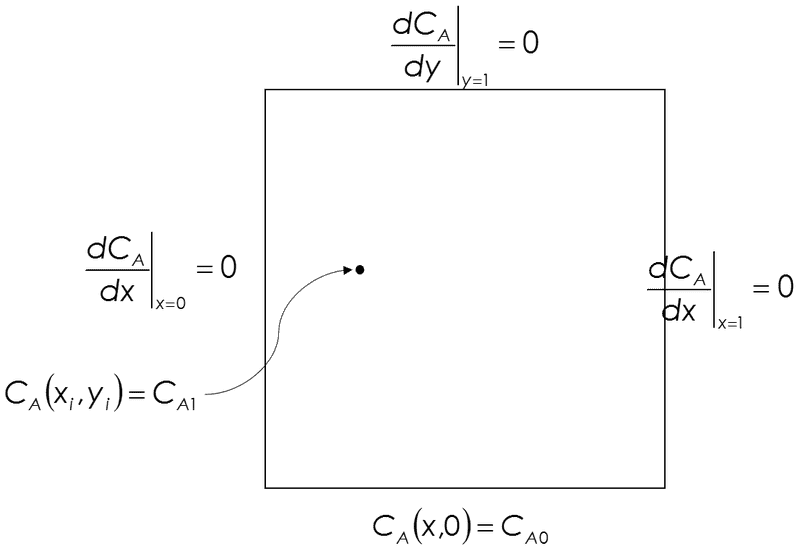
Basically this is solving the Laplace equation with those insulated boundaries except it has that point diffusing its value across the plane. I know how to solve the Laplace equation part. The problem is that I do not know how to solve the Laplace equation WITH a single point in there located at point (x_i, y_i).

While I have no problem in trying to solve this using numerical analysis, I am totally clueless how to solve this analytically. Where should I start? What should I do?

 

[Gallo]

It seems you are asking too much. The solution is uniquely determined by the boundary conditions. Once found a solution you can check if it is consistent with the value you have at ##(x_i,y_i)##.

 

[maistral]

What?? How could it be asking too much?

I said it clearly I guess. I don't know where to start at all. If that point C_A1 located at point (x_i, y_i) had not existed then obviously the solution for the PDE is just C_A0.

I have no idea how to incorporate that point diffusing its values everywhere on C_A0 that's why I'm asking.

 

[maistral]

Apparently this is Laplace equation with a dirac delta function on a certain coordinate. So apparently this involves Green's functions.

Who is this Green? Help?

 

[Chestermiller]

Let's sneak up on it. Suppose that, rather than being in a small finite domain of a square, the system were infinite in extent, and, rather than the concentration being CA1 at a point, it would be CA1 on a small circle of radius a. And suppose that, far from the circle, at infinity, the temperature would be CA0.

Chet

 

[Fred Wright]

I suggest you write the eigenvalue equation$$\Delta\phi+\lambda\phi=f$$where f is the diffusion function. First solve the homogeneous equation$$\Delta\phi + \lambda\phi=0$$by separation of variables and use the boundary conditions to find ##\phi_m\left (k_xx\right )## and ##\phi_n\left (k_yy \right )## and ##\lambda_{mn}=k_x^2+k_y^2##.
Introduce a trial function$$ \phi\left (x,y\right )=\sum_n\sum_m A_{mn}\phi_m\left (k_xx \right )\phi_n\left (k_yy \right )$$
and substitute in the equation$$\Delta\phi+\lambda_{mn}\phi=f$$
Multiply both sides of the equation by ##\phi_m\phi_n## and integrate to solve for ##A_{mn}##.

 

[maistral]

Thanks for the replies. But I gave up trying to get an analytical solution due to time constraints and killed the problem using a numerical attack. Lol